Hi Ned,

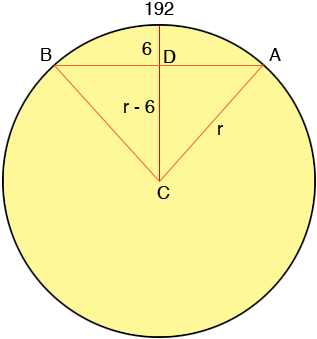
In my diagram if the measure of the angle BCA is θ radians then the length of the arc AB is given by r × θ and hence

192 = r × θ

Also from triangle DCA

cos(θ/2) = (r - 6)/r

Putting these two equation together gives

cos(192/(2r)) = (r - 6)/r or
cos(96/r) = (r - 6)/r

Unfortunately this equation can not be solved algebraically for r, the best you can do is approximate r. If you let

f(r) = cos(96/r) - (r - 6)/r

then you are looking for a root of f(r), that is a value of r so that f(r) = 0.

One approximation technique is newton's method but even here there are some pitfalls. Newton's method requires an initial guess and because of the oscillatory nature of the cosine function your equation has multiple positive roots and a poor initial guess might lead you to the wrong root. Since the sagitta is so small, we know that θ < π radians, so given that the arc is 192, then r ≥ 192/π, which provides us with a suitable initial guess for newton.

Newton's method applied to your problem yields r = 767 inches and hence θ = 192/767 = 0.2503 radians which is 45.05 degrees.

Stephen La Rocque and Harley Weston