Jasmine,

I am going to show you how to approach this problem using a similar function.

f(x)= - x² --> find f^-1[x], than state if its a function

I am first going to write the relationship as

y = - x²

so x is the input variable (is in the domain) and y is the output variable (is in the range). The inverse relationship interchanges the roles of x and y so it is given by

x = - y².

Putting it in the more conventional form, that is "solving for y" gives

y = ±√(-x).

The term (-x) under the root sign tells me that x must be zero or negative so the domain of this relationship is all x with x ≤0. It's also not a function, for example if x = -9 then

y = ±√(-(-9)) = ±√9 = ±3.

I think of these problems geometrically. When you tell me the function is y = -x² I see its graph

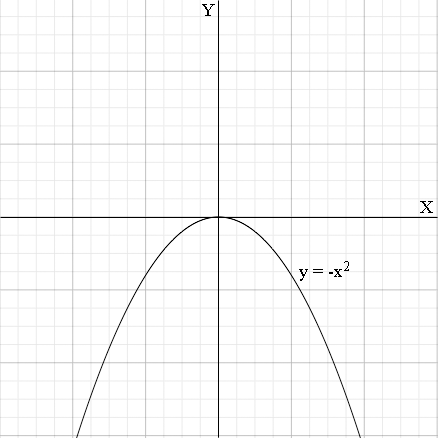
Graphing the inverse relationship means interchanging the X and Y axes and placing the resulting graph in standard position (see the video)

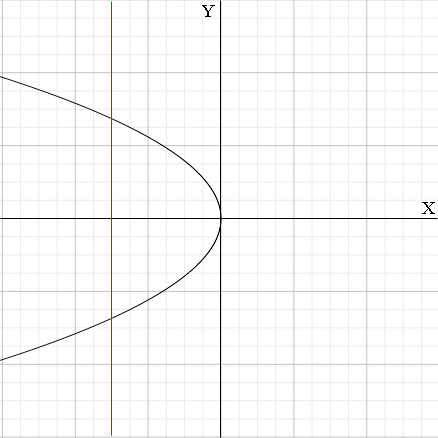
This is not the graph of a function. The red line shows that it doesn't pass the vertical line test.

I hope this helps,
Harley