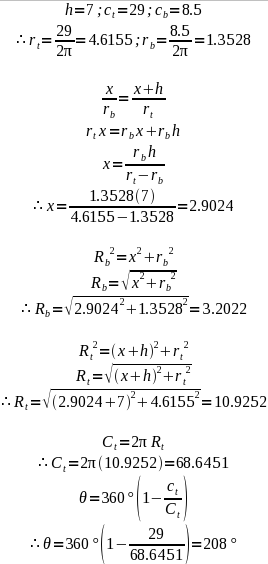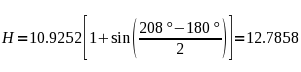A 3D cardboard cupcake - Math Central

HOME

Math Central

Quandaries & Queries

Question from Margaret, a student:

Hi,
I'm an art student and I'm attempting to build a 3D cupcake out of cardboard.
I want it to have a circular base of 8.5 inches and sides that are 7'' tall and slope outward so the top of the base is 29'.
The top with the frosting would be a detachable lid made from a cone with a base circumference of 29".
My problem is how to cut the side so they will slope out, I'm pretty sure there needs to be a curve, however I don't how to calculate the degree of it.
Ideally I want the sides to be a single piece of cardboard.
I also don't know how to calculate the arc needed to make a cone who's circular base's circumference is 29''.
Thanks,
Margaret

Hi Margaret. The cardboard pattern will be curved, you are right.

Take a look at this similar problem with diagrams that I solved awhile ago:
http://mathcentral.uregina.ca/QQ/database/QQ.09.06/s/mike1.html

Here's the math for your situation, based on the analysis and diagrams in that earlier problem:

The important results are: radius of the outer circle of the pattern is 10.9252, radius of the inner circle is 3.2022 and the angle is 208 degrees.

Thus, the appropriate shape is this:

pattern

To make this pattern on cardboard, I'll first figure out the overall height:

And of course the width is just the outside diameter, so the width is 2(10.9252) = 21.8904.

So cut a cardboard rectangle 21.8904 by 12.7858 inches (round this off as you see fit!), then locate the center of the circles by going to the middle of the sheet left/right, and drop down from the top 10.9252 inches.

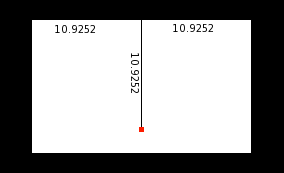
cardboard1

Use a compass (use string if you don't have a compass) and draw the outside circle using the radius 10.9252 inches. Then draw the inside circle with radius 3.2022 inches.

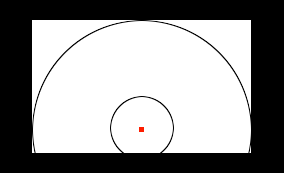
cardboard2

Finally draw straight cut lines from the center to the point where the outside circle touches the bottom of the cardboard.

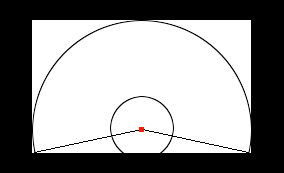
cardboard3

Then cut out your pattern and roll it up.

cardboard4

Please do email us a photo of the cupcake when you have it put together!

Hope this helps,
Stephen La Rocque.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.