| |||
| Math Central | Quandaries & Queries |
|
Question from Melissa: Is there a simple way to calculate how many labels are left on a roll? I thought there was a way to look at the individual label length, the label thickness and the core diameter and then measure the overall diameter to calculate how many pieces were left, but I'm struggling. I've seen a tool before- I thought we called it a circle calculator, but those parameters were all that I needed to input to spit out the correct count. I never saw what was behind the scenes for this calculation. Ie factoring in revolutions or the number of pieces on each layer, etc. Please let me know if you have any suggestions. Any assistance will be greatly appreciated!!! Thanks! |
Hello Melissa,
I will provide some guidance for you to develop a formula for yourself. Let’s draw a picture:
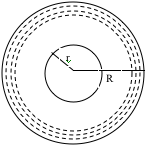
If the thickness of each layer is relatively small we can simplify the situation by treating each layer as a circle (technically a ring, or annulus). If we know the thickness of the roll and the thickness of each layer then we can determine how many layers are left : ![]()
Where Δ is the thickness per layer. Chances are that this number is not an integer, so for simplicity sake let’s round it to the nearest integer and call it, m. (ie m ≈ ![]() )
)
As more layers are peeled off the length of the layers decreases. Since the layers are circular, the length of the first is 2πR, the second 2π(R - Δ), third is 2π(R - 2Δ), and so on m many times [ending on 2π(r + Δ)].
The total length is obtained by adding up the lengths of the individual layers. Finally, if we find the length per label (taking spaces into account if applicable) we can determine a good estimate for the number of labels remaining.
Try to simplify the long sum. Good luck.
Tyler
Melissa,
Another approach is to calculate the length of "paper" remaining on the roll using the method I showed in the answer to a previous question. You then can use the number of labels per unit length to estimate the number of labels remaining.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.