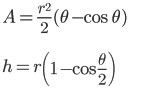| |||
| Math Central | Quandaries & Queries |
|
Question from Emily, a student: A cylinder is lying on it's side and being filled with water at a constant rate. Let the current height of water be t=0. When t=4, the cylinder is half full. When t=12, the cylinder is completely full. When is the rate of the height change increasing? |
Hi Emily,
The tricky part of a question like this is knowing the characteristics of a circular segment.
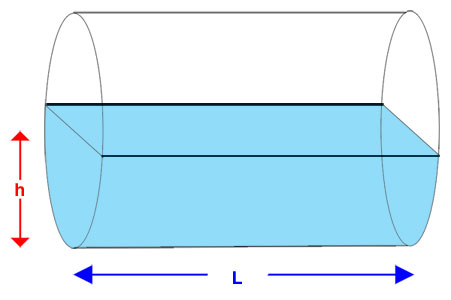 |
First we need only to consider the ends of the cylinder because the length will remain constant no matter how deep the water is. |
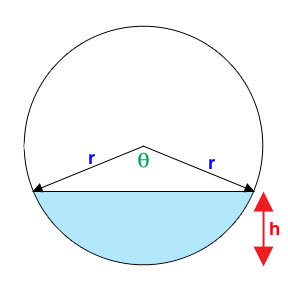 |
Draw radii to the end points of the chord that represents the water level. We can see that height and area of the circular segment depend on the angle between the radii. Area and height can be determined by the following relations:
|
For further help on related rates check out a similar question about a water trough.
Hope this helps,
Janice
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.