Hi Grant,

I redrew the diagram you sent and added some labels.

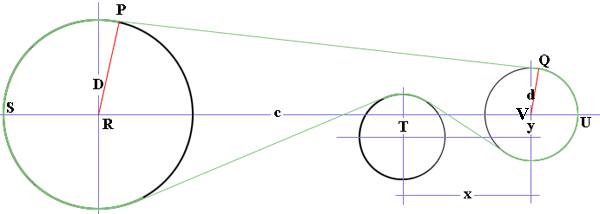
A few years ago I answered a similar question for a system involving two pulleys. You can use the same technique to find the length of the belt between $P$ and $Q.$ Using your notation I get

\[|PQ| = \sqrt{c^2 - \left(\frac{D-d}{2}\right)^2}.\]

Again from the technique in the earlier problem

\[\angle PRU = \angle QVU = tan^{-1}\left(\frac{|PQ|}{\left(\frac{D - d}{2}\right)}\right).\]

If you measure the angles in radians then $\angle SRP = \pi - \angle PRU$ and you can then find the lenghs of the belt sections from $S$ to $P$ and $Q$ to $U$ using the fact that the length of an arc of a circle is radius of the circle times the measure of the angle in radians.

Next look at the section between the large pulley and the tension pulley.

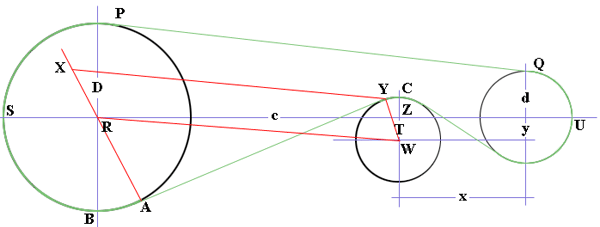
$R$ and $W$ are the centers of the two circles and $XY$ is parallel to$RW.$ Triangle $ZRW$ is a right triangle, $|WZ| = y \mbox{ and } |ZR| = c - x$ and hence Pythagoras theorem can be used to find the distance between the centers, $|RW|.$ Triangle $XAY$ is also a right triangle, $|YX| = |RW|$ and $|XA| = \frac{D + T}{2}$ and hence the length of belt $AY$ can be found using Pythagoras theorem.

Since triangle $ZRW$ is a right triangle the measure of angle $ZRW$ can be found fron the inverse tangent function. Likewise $\angle YXA = \angle WRA$ can be found from the inverse tangent function. Thus we have $\angle ARS = \pi - \angle ZRA$ and we can find the length of belt from $S$ to $A.$ Furthermore $\angle YWC = \angle ARB = \frac{\pi}{2} - \angle ZRA$ and thus we can find the length of belt from $Y$ to $C.$

A similar construction can be used to find the length of the remaining piece of the belt from $C$ to $U.$

Harley