Building a custom range hood

HOME

Math Central

Quandaries & Queries

Question from Bill:

I found another similar question in your Q&Q but it didn't answer my problem, so...

I'm building a custom range hood for a customer with special order material that matches
their newly installed cabinets and I need it to be perfect. The hood is basically a pyramid
but the 4th side is the flat wall at the back and a flat, rectangular top. I need to calculate
the bevel and miter of the three sides but I never was very good with geometry functions
(although I am fairly good with other math fields). I either need the calculations from you
at least (shudder) a formula or set of formulas so that I can calculate them myself.

Here are the dimensions that I have (in inches)...

Base - 29 15/16" x 17 1/4"
Top - 12" x 6"
Front Panel Length (from base to top) - approximately 20" (can be modified as needed)
Side Panel Length (from base to top) - approximately 18 7/8" (again can be modified as needed)
Front slope is approximately 25 degrees
Side slope is approximately 21 degrees

Any help finding the bevel/miter of the two front corners where the sides meet the front panel would be greatly appreciated.

Thanks in advance,
Bill

Hi Bill,

I think you are referring to Soren's question about the roof on an octagonal birdhouse. I used a similar method to approach your question.

In my diagram $|AB| = 17.25, |BE| = 29.9375, |DC| = 6 \mbox{ and } |CF| = 12,$ all in inches.

hood

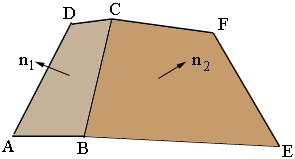
The distance from the edge $|BE|$ to the edge $|CF|$ is 20 inches which gave me a height of 16.5359 inches. This is the vertical distance from the base to the top. $n_1$ and $n_2$ are unit vectors that are perpendicular to the faces $ABCD$ and $BEFC.$ The angle between these vectors has the same measure as the angle between the faces $ABCD$ and $BEFC.$

I used Wolfram Alpha to do the calculations I needed. Below are the inputs and outputs.

Cross[{17.25, 0, 0},{11.25, 8.9688, 16.5359}]

{0, -0.8790, 0.4768} (This is the vector $n_1.$)

Cross[{11.25, 8.9688, 16.5359},{0, 29.9375, 0}]

{-0.8268, 0, 0.5625} (This is the vector $n_2.$)

ArcCos[{0,-0.8790,0.4768}.{-0.8268,0,0.5625}]*180/Pi

74.4428 (This is the angle between the faces $ABCD$ and $BEFC$ in degrees.)

Thus you should set the blade of your saw to 74.4428/2 degrees which is approximately 37.25 degrees.

I hope this helps,
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.