Hi John,

In the crayfish trap example Steve was constructing a full cone but you want a truncated cone. A better example would be Fluer's question about a lamp shade. I drew a diagram (not to scale) using the same notation as in the lampshade problem so that you can compare them.

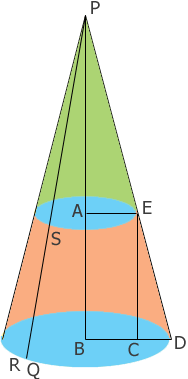
You have $|AE| = 0.5$ inches, $|BD| = 1.75$ inches and $|AB| = 9.5$ inches. Triangles $BDP$ and $CDE$ are similar and hence

\[\frac{|PB|}{1.75} = \frac{9.5}{1.75 - 0.5}\]

and hence

\[|PB| = \frac{9.5}{1.25} \times 1.75 = 13.3 \mbox{ inches.}\]

Pythagoras theorem applied to triangle $ECD$ yields

\[|ED| = \sqrt{9.5^2 + 1.25^2} = 9.58 \mbox{ inches.}\]

Similarly triangle $PBD$ is a right triangle so

\[|PD| = \sqrt{13.3^2 + 1.75^2} = 13.42 \mbox{ inches.}\]

Now slice the diagram from P to Q and roll it out to form a sector of a circle.

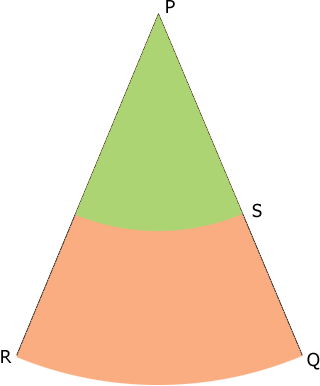
The circumference of the circle with centre $P$ and radius $|PR| = |PD| = 13.42$ inches is $2 \pi \times 13.42$ inches and the arc from $R$ to $Q$ is the circumference of the circle that forms the base of the wind sock. Thus the length of the arc from $R$ to $Q$ is $2 \pi \times 1.75$ inches. Hence the measure of the angle $QPR$ is

\[\frac{2 \pi \times 1.75}{2 \pi \times 13.42} \times 360^o = 47^o\]

At this point I suggest that you check my arithmetic and then make a paper copy. You may want to make the central angle larger than $47^o$ to give some overlap in order to stitch the wind sock together.

Penny