Hi Ralph,

When you say the 2x4 pieces are next to each other are you looking to make something like the diagram in mathcentral.uregina.ca/QQ/database/QQ.02.06/martin1.html

Harley

Yes I am but a circle rather than an octagon. Would the angle each side of the 2x4's need to be the same angle as the circle?

Ralph

The circumference of a circle of radius 10 inches is $2 \times \pi \times 10 = 62.83$ inches. Your lengths of 2x4 are 4 inches long and $\large \frac{62.83}{4} = 15.7$ and hence you will need 16 lengths of 2x4.

Below is a sketch of one of the 2x4 lengths (my diagram is not to scale).

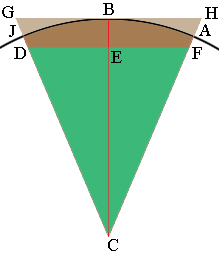
There are 16 of these around the circle and $\large \frac{360}{16}= 22.5$ and hence the measure of the angle GCH is $22.5^o$ and the measure of the angle BCH is $11.25^o .$ The circle has radius 10 inches and C is its center so the lengths of CJ, CB and CA are each 10 inches.

$ \tan(BCH) = \large \frac{|HB|}{|BC|}$ and hence $|HB| = 10 \times \tan(11.25) = 1.99$ inches and hence $HG| = 2 \times 1.99 = 3.98$ inches, almost exactly 4 inches.

The measures of angles CHB, HBC and BCH sum to $180^o$ and we know that HBC is a right angle and the measure of angle BCH is $11.25^o$ and thus the measure of angle CHB is $78.75^o.$

Cut each end of 16, 4 inch 2x4s at an angle of $78.75^o.$ Fit them together to form a 16-gon. To form a circle you will need to remove the approximately triangular pieces HBA and BGC. These are not large as AH is approximately $\large \frac{3}{16}$ inches.

Harley