Hi Tom,

There is no reason that the central angle needs to measure less than 180 degrees.

I think that one of the examples on Math Central that you might have found confusing is my response to Fleur who was constructing a lampshade. I have copied the images from that page so that I can easily refer to them.

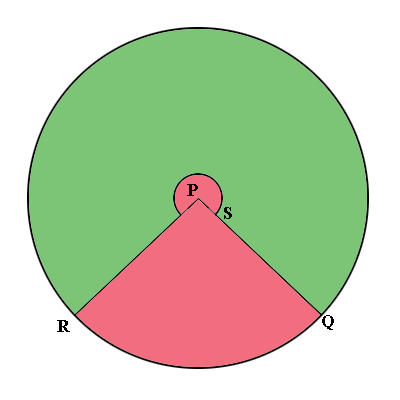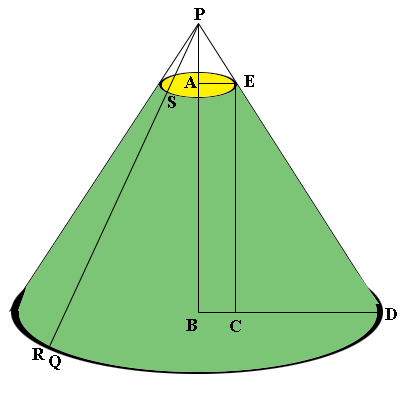
The green lampshade is on the left and the template to form it is on the right. I used the green colour to indicate which part of the image on the right is to be used to form the lampshade. When I made the calculations I was focused on the pink piece to be removed so the central angle I calculated was the central angle of the pink section which turned out to measure 142 degrees. I could just as easily have calculated the central angle of the green segment on the right which, as you observed, would be 360 - 142 = 218 degrees. Let me do that calculation.

From my response to Fleur we know that $|PR| = |PD| = 33$ cm and $|BD| = 20$ cm. Thus the circumference of the base of the lampshade measures $2 \pi \times 20$ cm. On the template on the right this is the length of the arc measured counterclockwise from Q to R. Since $|PR| = 33$ cm the circumference of the outside circle on the right measures $2 \pi \times 3$ cm. Hence the central angle of the green sector on the right measures

\[\frac{2 \pi \times 20}{2 \pi \times 33} \times 360 = 218 \mbox{ degrees.}\]

I hope this helps,
Penny