HI Mia,

I labeled the vertices of the diagram you sent and added two lines.

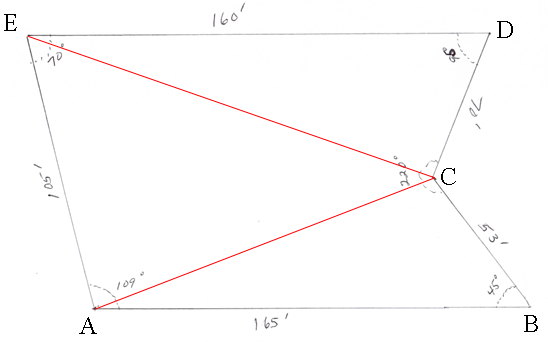
Your diagram bothers me somewhat as the measure of the angle at $D$ is given as $95^o$ and yet in the diagram it is more like $65^o$ or $70^o.$ From the other angles given the value of $95^o$ for the measure of the angle at $D$ is reasonable so I am going to proceed assuming the angle measures and side lengths in the diagram are correct.

No you can't add the lengths of $BC$ and $CD$ to calculate the area. You can however partition the lot into non overlapping pieces, calculate the areas of the individual pieces and add them to get the area of the lot. I have made a partition by drawing the lines $AC$ and $EC$ to subdivide the lot into three triangles.

I will calculate the areas of the three triangles using Heron's Formula. Heron's Formula lets you calculate the area of a triangle if you know the lengths of the three sides. Hence to complete the problem I need to find the lengths of $AC$ and $EC.$ This I will do using the Law of Cosines.

Look first at the triangle $ABC.$ By the Law of Cosines

\[|AC|^2 = |AB|^2 + |BC|^2 - 2 |AB||BC| \cos\left(45^o\right)\]

or

\[|AC|^2 = 165^2 + 53^2 - 2 \times 165 \times 53 \times 0.70711 = 17666.65 \mbox{ square feet}\]

and thus

\[|AC| = \sqrt{17666.65} = 132.92 \mbox{ feet.}\]

In a similar fashion you can see that $|EC| = 180.15 \mbox{ feet.}$

Now apply Heron's formula to the triangles, $ABC, ACE$ and $ECD.$ I am going again to focus on triangle $ABC.$ In this triangle $s = \large \frac{165 + 53 + 132.92}{2} \normalsize = 175.46 $ feet and thus the area of the triangle $ABC$ is

\[\sqrt{175.46 \times (175.46 - 165) \times (175.46 - 53) \times (175.46 - 132.92)} = 3092.1 \mbox{ square feet.}\]

In a similar fashion the area of triangle $ACE$ is 6914.7 square feet and the area of triangle $CDE$ is 5578.7 square feet.

Harley