Michael,

"Odd shaped lot" is exactly the correct subject line. The shape is important as well as the side lengths. To specify the shape I need the measures of the angles. Look at
http://mathcentral.uregina.ca/QQ/database/QQ.09.06/s/martha1.php
to see an example.

If the plot plan has the bearings of the sides you can use our Surveyor's Formula at
http://mathcentral.uregina.ca/QQ/tools/surveyors_formula.html
to download an Excel spreadsheet that will help you calculate the area.

Harley

Michael responded

That made no sense to me. Here is the shape of the lot....
Michael

Michael,

I have added some lines and notation (in red) to the diagram you sent.

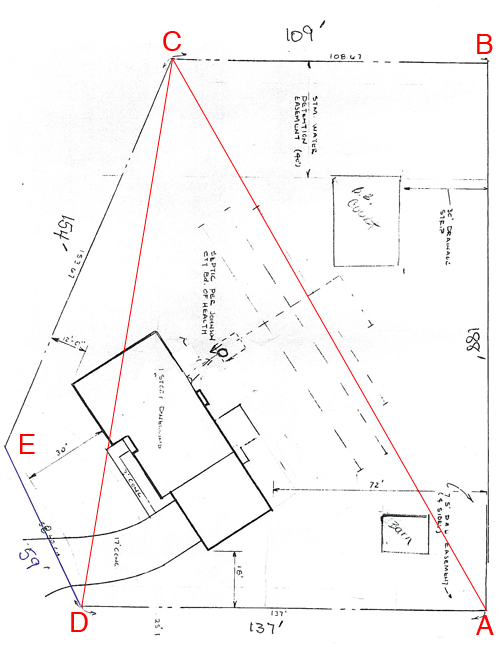
From the diagram it looks like the angles at $A$ and $B$ are right angles. I am going to assume these are right angles and based on this, calculate the area.

The region $ABCD$ is a trapezoid and its area is "the average of the lengths of the parallel sides times the distance between them" so in this case that is

\[\mbox{area of ABCD } = \frac{137 + 109}{2} \times 181 \mbox{ square feet.}\]

To determine the area of your property I want to add the area of the triangle $DCE.$ To calculate this area I need the length of $CD.$

Since the angle $ABC$ is a right angle I can use Pythagoras Theorem to find the length of $AC.$

\[|AC| = \sqrt{\left(109^2 + 188^2\right)} = \sqrt{47225} = 217.13 \mbox{ feet.}\]

I want now to determine the measure of the angle $BAC.$

\[\tan\left(BAC\right) = \frac{|BC|}{AB|} = \frac{109}{188} = 0.5798\]

and thus the measure of the angle $BAC$ is $\tan^{-1}(0.5798) = 30.10$ degrees. Hence, since the angle $DAB$ is a right angle the measure of angle $DAC$ is $90^o - 30.10^o = 59.90^o.$

Finally I can now use the Law of Cosines on the triangle $ACD$ to determine the length of $CD.$

\[|CD|^2 = |DA|^2 + |AC|^2 - 2 |DA||AC| \cos\left(DAC\right)\]

and thus

\[|CD|^2 = 137^2 + 217.13^2 - 2 \times 137 \times 217.13 \times \cos\left(59.90\right) = 36073.61 \mbox{ sq ft}\]

and thus $|CD| = \sqrt{36073.61} = 189.93$ feet.

Now that you have the lengths of the three sides of the triangle $DCE$ I can use Heron's Formula to calculate its area. I got the area of the triangle $DCE$ as 3964.14 square feet.

Add the area of this triangle to the area of the trapezoid $ABCD$ to determine the area of your lot is square feet. There are 43560 square feet in an acre so if you want the area in acres divide the area in square feet ny 43560.

Harley