Hi Levi,

Thanks for your kind words about our page about Mathematics at the Welding Shop. This was written by a grad 9 student in 1998. He is from Star City in Saskatchewan and went on a class visit to a welding shop. His task was to identify some of the mathematics he saw in the process of constructing cone shaped hopper bottoms for grain bins.

To answer your question imagine that your finished cone is as in the diagram below.

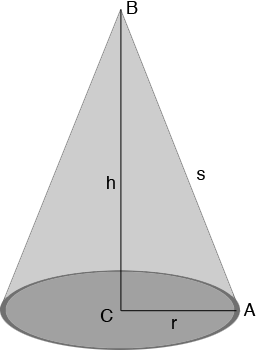
The radius of the base is $r$ units, the height is $h$ units and the slant height is $s$ units. If you slice along the line $AB$ and roll it out flat then you have a sector of a circle of radius $s$ units. In your situation you know $r$ and $h$ and you want to find $s.$ The key is that triangle $ABC$ in the diagram above is a right triangle and hence you can use Pythagoras Theorem which says that

\[|AB|^2 = |BC|^2 + |CA|^2\]

or

\[s^2 = h^2 + r^2\]

Hence

\[s = \sqrt{h^2 + r^2} \mbox{ units.}\]

I hope this helps,
Harley