Ray,

Are you sure you have worded the problem correctly? Look at Stephen's response to a similar question.

Penny

Ray wrote back

Hello Penny,

I think I stated it correctly. I heard it on the radio but maybe missed something. At any rate,
your drawing satisfies the problem and the solution for the outer circle is understood, BUT is there a way to deduce the area of the inner circle with the info given???

Thanks, Ray

Ray,

You can't determine the area of either circle just the area of the annulus between the circle, the region shaded light purple in Stephen's diagram. To convince yourself draw a line segment $AB$ with a given length and let $M$ be the midpoint of $AB.$ Draw a line $l$ through $M,$ perpendicular to $AB$ and let $C$ be any point in $l.$ Draw a circle with centre $C$ and radius $MC$ and another circle with centre $C$ and radius $CA.$

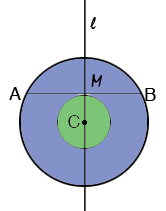
Now select a different point $C$ on $l$ and repeat the construction.

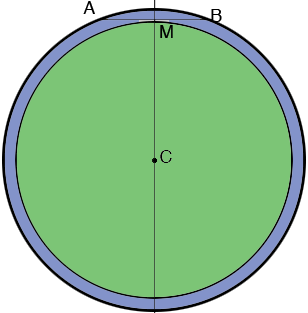
In the two diagrams the two small circles and the two large circles have quite different areas and yet, as Stephen showed, the regions between the two circles are equal in area.

Penny