| |||
| Math Central | Quandaries & Queries |
|
Question from Victoria, a student: find the area of a regular pentagon inscribed in a circle with radius 3 units |
Hi Victoria,
If you join each of the vertices of the pentagon to the center $C$ of the circle you will see that the pentagon is partitioned into five congruent isosceles triangles. I have labeled one of these triangles $ABC.$ Thus the area of the pentagon is 5 times the area of the triangle $ABC.$
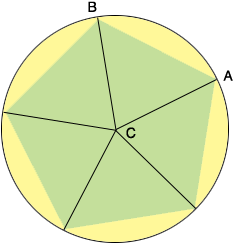
S\Also you can see that the measure of the angle $BCA$ is $\frac{360^o}{5} = 72^{o}.$ You can use the technique in my response to a question by Sela to find the area of triangle $ABC.$
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.