| |||
| Math Central | Quandaries & Queries |
|
Question from Steve: On your website, I was reading a question and your response from a girl named Angela in which you provided a formula by which her father, a welder, could figure out points on an arc corresponding to equal 3' intervals on a 30' chord where the vertex was 1' off the chord. Is there an equivalent formula when working with an ellipse? I suspect this change will make the calculations significantly more complex. I am building a deck that is half an oval, and would like to be able to mark out the perimeter by measuring the distance from regular intervals on the primary access to a corresponding point on the perimeter. I will then connect the points on the perimeter and cut a reasonably smooth arc. The length of the primary access will be 22' and width of the deck at the vertex is 9'. I would like to be able to know the distance from the primary axis to a point on the perimeter at equal intervals of 6" along the primary axis. Can you help? |
Hi Steve,
There is a solution to your problem that is easier than Stephen's solution to Angela's problem. The solution comes from the fact that an ellipse is the locus of all points in the plane such that the sum of the distances from each of the points to two fixed points is a constant. This is classical mathematical language so, what does it mean?
Drive two nails into a board. These are the fixed points called the foci. Cut a length of string longer than the distance between the foci. Tie the ends of the string to the nails. Place a pencil so the string forms a triangle with the pencil and the two nails the three vertices. Move the pencil, keeping the string taught and the curve traced by the pencil is an ellipse. At each point on the curve the sum of the distances from the pencil to the foci is a constant, the length of the string.
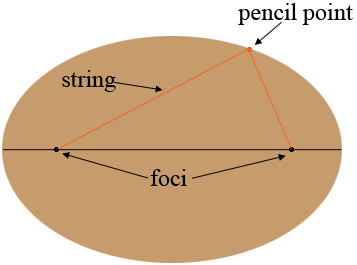
To draw the ellipse you want you need to know the length of the string and the position of the foci.
I redrew the ellipse and labeled some points.
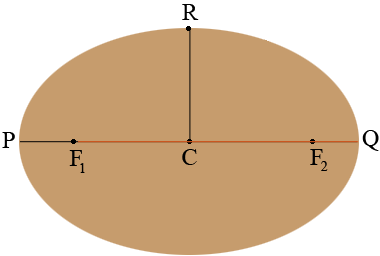
The point $C$ is the midpoint of the line segment $PQ.$ When the pencil is at the point $Q$ the string goes from $F_1$ to $Q$ and then back to $F_{2}.$ The distance from $Q$ to $F_2$ is equal to the distance from $P$ to $F_1$ and hence the length of the string is $|F_1 Q| + |QF_2| = |F_1 Q| + |PF_1| = |PQ|$ which in your case is 22 feet.
When the pencil is at the point $R$ in the diagram the string goes from $F_1$ to $R$ and then from $R$ to $F_{2}.$
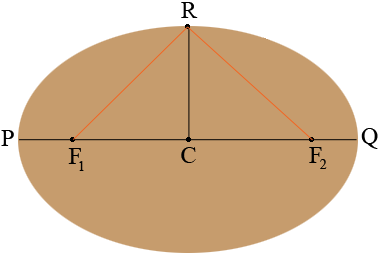
By the symmetry of the diagram the distances $F_1 R$ and $R F_2$ are equal and hence $|R F_2| = 11$ feet. You also know that $|RC| = 9$ feet. Suppose the distance from $C$ to $F_2$ is $x$ feet. Triangle $RCF_2$ is a right triangle and hence from Pythagoras Theorem
\[x^2 + |RC|^2 = |RF_2|^2 \mbox{ or } x^2 + 9^2 = 11^{2}.\]
Solving for x gives $x = 6.32$ feet which is very close to 6' 4".
Thus to draw your ellipse locate the midpoint $C$ of the straight side, measure 6" 4" each way to locate $F_1$ and $F_{2}.$ Pound a nail at these two points and tie a string between $F_1$ to $F_2$ so that the length of the string between the foci is 22 feet. Draw your half ellipse.
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.