Hi Dale,

I can show you an approach to take using the angle measurements you supplied. I am going to leave much of the calculation to you.

I drew a diagram of your pentagon, not to scale, labeled the vertices and added two lines.

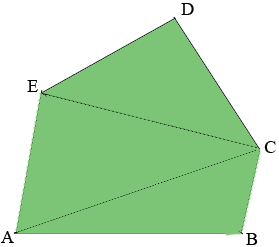
• $|AB| = 67$ feet
• $|BC| = 18$ feet
• $|CD| = 49$ feet
• $|DE| = 35$ feet
• $|EA| = 39$ feet
• Angle $EAB$ measures $80^o$
• Angle $ABC$ measures $100^o$

Using the Law of Cosines on triangle $ABC$ I get

\[|CA|^2 = |AB|^2 + |BC|^2 - 2 |AB| |BC| \cos\left(ABC\right)\]

or

\[|CA|^2 = 67^2 + 18^2 - 2 \times 67 \times 18 \cos(100^o) = 5231.8394 \mbox{ feet squared}\]

or

\[|CA| = \sqrt{5231.8394} = 72.33 \mbox{ feet.}\]

At this point use the Law of Sines on triangle $ABC$ to get

\[\frac{\sin(CAB)}{|BC|}=\frac{\sin(ABC)}{|AC|}\]

or

\[\sin(CAB) = \frac{|BC| \sin(ABC)}{|AC|} = \frac{18 \sin(100^0)}{72.33}.\]

and hence

\[CAB = \sin^{-1}\left(\frac{18 \sin(100^0)}{72.33}\right) = 14.19^{o}.\]

Since the measure of the angle $EAB$ is $80^o$ the measure of the angle $EAC$ is $80 - 14.19 = 65.81$ degrees.

Now you can again use the Law of Cosines on the triangle $EAC$ to find the length of $CE|.

At this point you have partitioned the pentagon into three triangles $ABC, CEA$ and $CDE.$ You know the lengths of the three sides of each of the triangles so you can use Heron's Formula to find the area of each of the triangles and the area of the pentagon is the sum of the areas of these triangles.

Since you seem to be somewhat sure of the measure of the angle $ABC$ you could modify it slightly, say to 97 degrees, making the measure of the angle $EAB$ 83 degrees, repeat the calculations and see how much effect it has on the area of the pentagon.

Write back if you need more assistance.

Harley