Hi Herm,

I drew a diagram looking down on the tray with the seven spheres in place. I coloured one of the spheres blue because I want to concentrate in it in a moment.

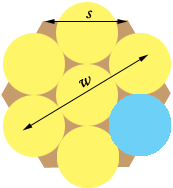
In my diagram $w$ is the width of the hexagon and $s$ is its side length. In a response to an earlier question Penny showed that

\[w = \sqrt3 \;s.\]

I am going to find $w$ which will then let you determine $s.$

My second diagram is a side view of the blue sphere with $D$ and $E$ on the tray. $C$ the center of the sphere and $EA$ one of the $0.75$ inch high sides of the hexagon.

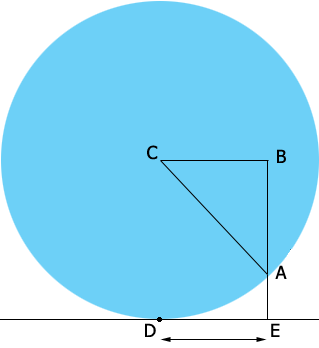
$|CA| = 3$ inches is the radius of the sphere, $|BA| = |BE| - |AE| = 3 - 0.75 = 2.25$ inches and triangle $ABC$ is a right triangle and hence Pythagoras' theorem tell us that

\[|BC|^2 + |AB|^2 = |CA|^2 \mbox{ or } |BC|^2 = 3^2 - 2.25^2\]

and hence

\[|DE| = |CB| = 1.9843 \mbox{ inches.}\]

Thus from the first diagram the width of the hexagonal tray is given by

\[w = 4 \times 3 + 2 \times 1.9843 \mbox{ inches.}\]

Harley

Herm wrote back

This is not a question, but rather a thank-you response to Harley Weston for providing a straightforward solution to my question. Harley kindly tackled the problem and provided an easy-to-follow solution, however, in generating the methodology Harley inadvertently used 3 inches as the radius instead of 1.5 inches. Thus, the result for ascertaining the width of the hexagon should be:

\[w = 4 \times 1.5 + 2 \times 1.0607\]

The "1.0607" value is calculated from the blue sphere in Harley's drawing as follows:

\[CA^2 = CB^2 + BA^2\]

\[1.5^2 = 2 \times (BA^2) \mbox{ [because CB = BA] }\]

\[2.25 = 2 \times (BA^2)\]

\[BA = \sqrt{1.125} = 1.0607 = DE\]

This problem has a very practical basis for me. I want to build a hexagonal tray to accommodate 7 official ML baseballs, which have a diameter of 2 15/16 inches.

THANKS again and all the best!

Herm

Thanks for the kudo Herm, I enjoyed responding. Thanks also for the explanation of the source of the problem. It makes more sense now.

Harley

Herm sent us a photo

Finally “finished” my baseball hexagon — just need to stain and varnish it (which may not happen for some time).

The circumference has 6 official baseballs — 2 from the AL (1 with Bobby Brown as the Commissioner and 1 with Gene Budig as the Commissioner), 2 from the NL (1 with Bill White as the Commissioner and 1 with Leonard Coleman as the Commissioner) and 2 from MLB (1 with Bud Selig as the President and 1 with Rob Manfred as President). Each of these baseballs has a diameter of 2 15/16 inches.

The center ball is a re-creation of the baseballs used in 1859-1860. These balls were made from dark-brown leather and stitched in the “lemon peel” arrangement. The diameter of the lemon peel baseball is larger than that of the current official baseball. Thus, the center lemon peel ball rests above the 6 circumferential balls.

It’s a nice display showing 140 years of baseballs.

I’m very pleased with it.

And, I thank you so much for providing the measurements needed to make the hexagonal tray such that the centers of the 6 circumferential balls are above the top of the tray. This was back in mid-January.

Thanks again, Harley, and all the best!

Herm