Hi Patrick,

I am assuming this is a circular arch.

If the length of a circular arc is $a$ units and the angle subtended by the arc, at the center of the circle is $t^o$ than

\[a = 2 \pi \; r \frac{t}{360}.\]

Thus you need to find $r$ the radius of the circle and the measure $t$ of the angle subtended by the arc.

In my diagram of your arc $C$ is the center of the circle, $A$ and $B$ are the ends of the arc and $P$ is its apex.

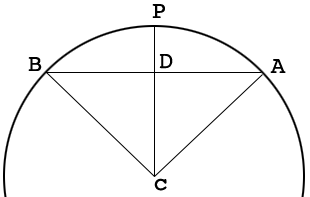
$|AC| = r, |PD| = 30$ inches and $|DA| = 24$ inches. Thus $ADC$ is a right triangle with sides of length $|AD| = 24$ inches and $|DC| = r - 20$ inches. Its hypotenuse is of length $r$ inches. Use Pythagoras Theorem to solve for $r.$ Use a trig function to find the measure of angle $DCA.$

I hope this helps,

Penny