Hi,

You didn't say which two sides are the parallel sides. There is an interesting note on the Math Forum site concerning this. I am going to describe how you can find the area if you know which two sides are parallel.

Suppose the vertices of the trapezoid are $P, Q, R$ and $S$ and side lengths are $w, x, y$ and $z$ feet and the sides of length $w$ and $y$ feet are parallel.

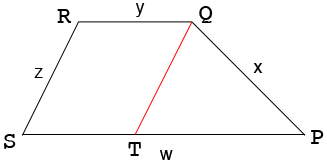
I added the line segment $QT$ which is parallel to $RS.$ Hence the trapezoid is partitioned into a parallelogram $QRST$ and a triangle $QTP.$ Hence the area of the trapezoid is the sum of the areas of the parallelogram and the triangle. $|ST| = y$ and $|TP| = w - y$ and the height of the triangle and the height of the parallelogram are equal so if you can find the height of the triangle $QTP$ you can find the area of the trapezoid.

I can show you two ways to find the height of the triangle $QTP.$

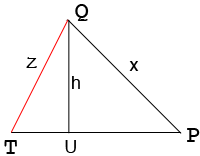
First method.

Drop a perpendicular $QU$ from $Q$ to meet $TP$ at $U.$

Let the $|TU| = t$ feet then $|UP| = |TP| - t$ then since $QTU$ and $QUP$ are right triangles, Pythagoras Theorem for these two triangles gives two equations in $h$ and $t.$ Solve for $h.$

Second method.

Find the area of triangle $QTP$ using Heron's Formula and us the fact that the area of this triangle is also $\large \frac12 \normalsize |TP| \times h$ to solve for h.

Once you have the area $A$ of the trapezoid in square feet type A square feet in acres into the Google Search window to convert this area to acres.

I hope this helps,
Penny