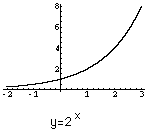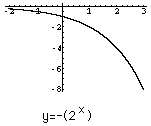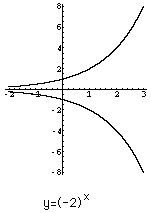| |||
| Math Central | Quandaries & Queries |
|
Question from Gonzalo: Hi, I'm sorry for deviating off the topic. This is not precisely a maths question, but it is formulated based on my maths curiosity. Fidgetting with my new graphic calculator, I started graphing things and had the idea to graph $y=(-2)^x.$ The next month I was at my friend's house at 1 a.m. reading some homebrew Dungeons and Dragons ruleset together when I remembered the function and slipped it into our conversation. My friend, who is also a little of a maths enthusiast, enjoyed the function, and we started analyzing it. Soon enough we arrived to the conclusion of there being a lot of complex numbers, in the function, the best way we came up with to graph it was graphing both $2^x$ and $(-2)^x$ and giving them both transparency to represent the "holes". Another cheaty way of representing it was in a three-dimensional space assigning the imaginary parts to z. Anyway, we didn't stop here and started graphing the derivatives and other related functions in 3D, showing very interesting numbers, coincidences, and properties. Even though we were starting to struggle to explain why such things happened, we had a lot of fun. It was 3 a.m., two hours passed by incredibly fast, we spent another hour reading the remaining pages of the ruleset and went to sleep. The next morning we agreed how much fun it was and how we should repeat it. Today I surfed the web and ended up in this web page: mathcentral.uregina.ca/QQ/database/QQ.09.97/bokinac1.html This is the best channel of communication I could find. This article in math central is one of the only analysis I have seen regarding this kind of functions. The article has some interesting points and solves very well which points are complex and which aren't. It explains this last point in a much better way than the one me and my friend were able to put together. Having acquired this knowledge, my curiosity for this graph has grown, and I might be able to find with my friend some meaning to the coincidences we found. I know the person who answered the question and wrote this article is named Harley, and I was wondering whether I could get access to her contact info to talk with her/him about this function. Sorry for my English and hoping to hear from you soon,
|
Hi Gonzalo,
I reformatted the content of the page you mentioned since it was created some time ago, 1997, and is badly formatted.
Question:
During our math class last week we came across an equation that we could not graph we were wondering if you could help us try and graph it. The question is:
$y=(-2)^x$Hi Ken,
To deal with the function $y=(-2)^x$ you need to decide what values of x give a real number. Certainly if $x$ is an integer then $(-2)^x$ is real. Also if $x=1/3$ or $x=1/5$ then $(-2)^x$ is real but if $x=1/2$ then$(-2)^x$ is not real. In fact $(-2)^x$ is real if and only if $x$ can be written as $p/q$ where $p$ and $q$ are integers with no common factors other than 1 and $q$ is odd. If $x=p/q$ is such a rational number then $(-2)^x=2^x$ if $p$ is even and $(-2)^x=-(2^x)$ if p is odd.
To see the graph of $y=(-2)^x$ first consider the graphs of $y=2^x$ and $y=-(2^x).$
The graph of $y=(-2)^x$ is then
What you don't see in the picture is that the graph has a large number of "holes". The only points on the graph have first coordinate x=p/q where p and q are integers with no common factors other than 1 and $q$ is odd. If $p$ is even the point with first coordinate $x=p/q$ is on the "upper" curve and is $p$ is odd the point with first coordinate $x=p/q$ is on the "lower" curve.
Cheers,
Harley
Your project is great. I hope I can be of some help.
First of all I was not very clear in my response above. I want to focus on $(-2)^{1/3}$ and think about complex numbers. I am looking for any complex number $z$ so that $z = (-2)^{1/3},$ in other words $z^3 = -2.$ As I indicated in my response above there is a real number that satisfies this requirement, namely $-2^{1/3}$ but that's not the only solution,
\[z = \frac{1}{2^{2/3}} \pm \frac{\sqrt{3} \; i}{2^{2/3}} \mbox{ are solutions also.}\]
You can verify this by expanding $z^{3}.$ For example expand
\[\left( \frac{1}{2^{2/3}} + \frac{\sqrt{3} \; i}{2^{2/3}}\right)^3 = \left(\frac{1}{2^{2/3}} + \frac{\sqrt{3} \; i}{2^{2/3}}\right)^2 \times \left(\frac{1}{2^{2/3}} + \frac{\sqrt{3} \; i}{2^{2/3}}\right)\]
to verify that its value is $-2.$
Does this help in your investigations? Write back if I can be of any further assistance.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.