Hi Guy,

In the diagram below from our earlier post you want to cut along the lines $QP$ and $RP,$ discard the pink piece and roll up the green piece to form the lamp shade.

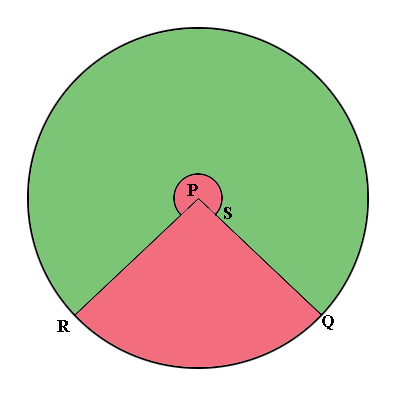
To complete the construction you need to know the measure of the angle $QSR.$ To determine this angle you need to use the symmetry of the circle and make a calculation.

Suppose the calculations earlier in this question had led you conclude that the distance from $Q$ to $R,$ counterclockwise around the circle is $\large \frac{3}{4}$ of the circumference of the circle. Thus the distance from $R$ to $Q,$ measured counter clock wise around the circle is $1 - \large \frac{3}{4} \normalsize = \large \frac{1}{4}$ of the circumference of the circle. In this case the symmetry of the circle leads us to conclude that the measure of the angle $QSR$ is $\large \frac{1}{4}$ of $360^{o}.$

In the earlier question the distance from $Q$ to $R$ measured counterclockwise around the circle is $2 \pi \; \times 20$ cm and hence as a fraction of the circumference of the circle that's

\[\frac{2\pi \; \times 20}{2\pi \; \times 33} = \frac{20}{33}.\]

Thus the distance from $R$ to $Q$ measured counterclockwise as a fraction of the circumference of the circle is

\[1 - \frac{20}{30} = \frac{13}{33}.\]

Again by the symmetry of the circle the measure of the angle $QSR$ is $\large \frac{13}{33} \normalsize \times 360^o = 142^{o}.$

I hope this helps,
Penny