Subject: parabolic mirrors

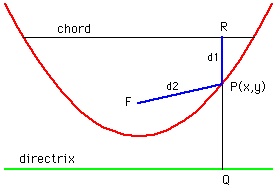
Hi, my name is Megan. I am a grade 12 student at RCS-Netherwood in New Brunswick. My question: Consider a ray of light that passes through a chord of a parabola (the chord is above the focus and parallel to the directrix), hits the parabola at a point (x,y) and is reflected through the focus. If d1 is the distance from the chord to the point of incidence (x,y) and d2 is the distance from (x,y) to the focus, can you prove that the sum of the distances d1+d2 is constant, independent of the particular point of incidence.(please/thank you)

If you look at the right diagram your problem is straightforward.

Since the point P(x,y) is on the parabola |FP|=|PQ|. Thus d1+d2 is the distance from R to Q, that is the vertical distance from the chord to the directrix which is the same for every ray of light. You might want to look at the Resource Why are satellite dishes parabolic?. This resource has a proof that the ray of light does get reflected through the focus and also points out one reason why the property in your problem is important.

Cheers
Penny