Why are satellite dishes parabolic?
Harley Weston,
Department of Mathematics & Statistics,
University of Regina
The purpose of a satellite dish is to collect the signal from the satellite and focus it onto the receiver. To determine the optimal shape for the dish, you need to find a surface that will reflect the incoming signal to the receiver from every point on the dish surface.
From physics we know that a ray striking a planar surface reflects so that the angle of reflection is equal to the angle of incidence. If the surface is curved then the same physical law is true, where the reflection plane is the plane which is tangent to the surface at the point of contact. To show that the parabolic shape is optimal for a satellite dish you need to know this physical fact, the definition of a parabola, some elementary geometry and one fact from calculus.
A parabola is the locus of points which are equidistant from a fixed point, the focus, and a fixed line, the directrix. To find the equation of such a curve construct a coordinate system on the plane so that the focus is the point (0,p) and the directrix is the horizontal line y = -p. A point (x,y) is thus on the curve if and only if the distance from (x,y) to (0,p) is equal to the distance from (x,y) to the line y = -p. Equating the squares of these distances (so that you don't have to deal with square roots), this requirement is
(x-0) 2 + (y-p) 2 = (y+p) 2.
Expanding both sides and simplifying gives
4 p y = x 2 or
as the equation of the parabola.
Suppose that the satellite is directly overhead and thus the parabola constructed is pointed at the satelite. The satellite is far enough away that we can be assume the signal is approaching the dish vertically. Suppose that a particular signal strikes the dish at the point P with X-coordinate a, then the point P is (a, a2/(4p)). Extend the vertical line through P to meet the directrix at Q, which then has coordinates (a,-p). The focus has coordinates (0,p) and thus the midpoint S of the line segment FQ has coordinates (a/2,0) and is therefore on the X-axis.
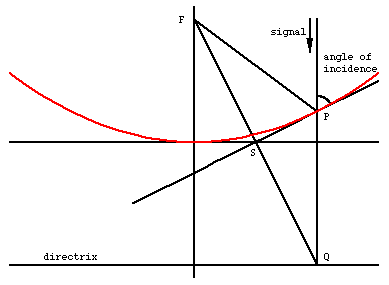
The fact needed from calculus is that the tangent line to the parabola at the point P has slope 2 a/4 p, and thus the equation of the tangent line at this point is
To find the point where this tangent line intersects the X-axis set y = 0 and simplify to find that x = a/2. But this is S, the midpoint of the line segment FQ. Since |FP| = |PQ| (definition of a parabola), the triangles FPS and QPS are congruent and therefore the angles FPS and QPS are equal. But the angle QPS is equal to the angle of incidence and thus the signal will reflect along the line PF and pass through the focus. Placing the receiver at the focus of the parabola will thus result in a dish that will reflect all signals from the satellite to the receiver.
The solution to a problem on
parabolic mirrors sent to Quandaries and Queries implies that every
signal from the satellite that strikes the dish and is thus reflected to the
focus travel the same distance regardless of where it stikes the dish. This is
an important property of the parabola as it assures that all signals reach the
focus "in phase" and do not interfere with each other.