Date: Wed, 24 Mar 1999 11:22:26 -0600 (CST)
Subject: complex numbers/polar coordinates

Name: Kate

Who is asking: Student
Level: Secondary

Question:
What is the relationship between complex numbers and polar coordinates?

Hi Kate
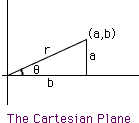
Complex numbers can be expressed using the idea behind polar coordinates and this representation turns out to be very useful. The idea is as follows:

 
  Complex numbers can be written in the form a+ib where a and b are real numbers. This gives rise to a graphical way to represent complex numbers in what is called the complex plane. Draw a coordinate system as you would for the Cartesian plane but label the horizontal axis the real axis and the vertical axis the imaginary axis. The complex number a+ib is then representated in the complex plane by the point with coordinates (a,b).  
  If you introduce the polar coordinates notation into the Cartesian Plane as in the diagram then a/r = cos() and b/r = sin() so a = r cos() and b = r sin(). Hence the complex number a+ib can be written r cos() + i r sin() or more compactly r (cos() + i sin()).
   You can see a use of this way of expressing complex numbers in the answer I gave to a teacher who asked about the square root of i.

I hope this helps
Harley

 
 
Go to Math Central

To return to the previous page use your browser's back button.