Sender: Roger
How many cannonballs can be stacked in a triangular pyramid?
Hi Roger
If you stack cannonballs in a triangular pyramid then the top layer has one cannonball, the second layer has 3 cannonballs, the third layer has 6 cannonballs, ... These are triangular numbers. (See an earlier note in the Quandaries and Queries section called Triangular Numbers.) The nth triangular number is T(n) = n(n+1)/2 which you should recognize as the binomial coefficient 
which is the number of ways of selecting 2 things from n+1 things.
Thus the number of cannonballs in a triangular pyramid is
- 1 if the pyramid has 1 layer
- 1+3 if the pyramid has 2 layers
- 1+3+6 if the pyramid has 3 layers
- ...
- 1+3+6+...+n(n+1)/2 if the pyramid has n layers
There is a nice way to exprress this number which you can see as follows. Suppose that n+2 people are standing in a row and you are to walk down the row and select three of them. You can do this in
ways.
The third person selected could be person number 3, person number 4, person nunber 5 ... up to person number (n+2).
- If the third person select is number 3 then the first two selected were 1 and 2 which could only be done in 1 = T(1) way.
- If the third person select is number 4 then the first two were selected from 1, 2, and 3 which could be done in
= T(2) ways.
- If the third person select is number 5 then the first two were selected from 1, 2, 3 and 4 which could be done in
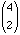= T(3) ways.
- ...
- If the third person select is number n+2 then the first two were selected from 1, 2, 3 ... n+1 which could be done in = T(n) ways.
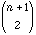the number of ways of selecting 3 items from n+2 items is T(1)+T(2)+T(3)+...+T(n). Hence the number of cannonballs in a triangular pyramid that is n layers high is .
Cheers
Penny
To return to the previous page use your browser's back button.