Is there a formula for the expansion of (a+b+c) to the nth power? Does it have to do with Pascal's triangle?

Student is asking.

Hi Suraj,

Pascal's triangle is used to find the binomial coefficients that are needed for expanding the binomial (a + b)ⁿ. The binomial coefficient n choose k is usually written or sometimes  _nC_k. where

In the binomial expansion of (a + b)ⁿ each term is a constant times a^kb^n-k where the constant is n choose k. that is

(To see the first and last coefficients an binomial coefficients you need to use the conventions that 0! = 1 and x⁰ = 1.)
   In the expansion of (a + b + c)ⁿ each term is a constant times a^pb^qc^r where p + q + r = n. In this expansion the coefficient of a^pb^qc^r is . These are called multinomial coefficients. Thus (a + b + c)ⁿ is the sum of all terms of the form

where p + q + r = n. For example

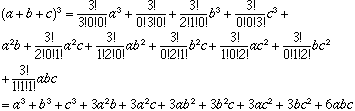
Cheers,
Penny