my name is michael moran i think there is a contridiction in imaginary numbers

we learn:

i squared = -1

but

i squared = root(-1)* root(-1)
= root( -1*-1)
= root(1)
= 1
-1 doesn't = 1

can you help me with my question

Problems of that type confused a lot of mathematicians of the last century. Here is another example:

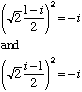
So, which should be the root of -i?

With roots of positive real numbers, the convention is that root(a) means the POSITIVE root of a, and this removes all possible ambiguities about what root(a) means. In particular, this is what makes an identity like root(a) * root(b) = root(a*b) valid: There is no question that you are talking about positive roots all the way through.

With complex numbers, there is no longer the possibility of making such a convention for the root of a number. This implies that an expression such as root(-i) is ambiguous, because it is not clear whether it means root(2)*(i-1)/2 or root(2)*(1-i)/2. Also, the identity root(a) * root(b) = root(a*b) is no longer valid for complex numbers (because "root" is undefined). Therefore, in your calculation, the step root(-1)* root(-1) = root( -1*-1) is invalid, though it looks natural. That is why you seem to end up with -1 = 1, which is certainely false.

The moral of all of this is:
Do not say "THE square root of this complex number"
but rather "A square root of this complex number".