Subject: volume formula

secondary level(10-12)
Does anyone have a way to physically demonstrate how to explain the volume formula for a sphere? Or perhaps how to derive the formula without calculus?

gracias
kevin

Hi Kevin,

There is a geometric construction due to Archimedes which demonstrates what you ask. Archimedes himself considered this and similar constructions as his greatest works. A great place to find such historical notes is The MacTutor History of Mathematics archive. Go to the Biographies Index and under "A" look for Archimedes. A quote from this archive is "Archimedes considered his most significant accomplishments were those concerning a cylinder circumscribing a sphere, and he asked for a representation of this together with his result on the ratio of the two, to be inscribed on his tomb."

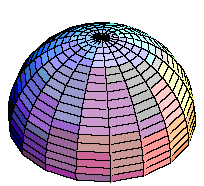
Start with a hemisphere of radius r and construct a cylinder of radius r and height r. The diagram below contains a cutaway view of the cylinder.

Figure 1

Now place an inverted cone with height r and base radius r inside the cylinder.

I am interested in the volume of the region between the cone and the cylinder.

Slice through both figures with a plane parallel to the base and at a height h units above the base. Peal back what you have cut off and look down from above. What you see on the left is a circular disk and on the right is a region between two concentric circles. I want to compare the areas of these two regions.

Figure 2

If the radius of the circle on the left is p then its area is pi times p2. The radius p can be found from a cutaway view of the hemisphere.

Figure 3

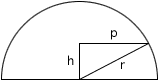
By the theorem of Pythagoras p2 = r2 - h2 and hence the area of the circular disk is pi(r2 - h2).

For the region between the concentric circles the radius of the outside circle is the radius of the cylinder,r. Since the radius of the base and the height of the cone are both r, a cutaway view of the cone inside the cylinder shows similar triangles with the height equal to the base. Hence the radius of the inside circle is h. Thus the area of the region between the concentric circles is pi*r2 -pi*h2 = pi(r2 - h2).

Figure 4

Therefore the areas of the two regions in figure 2 are equal.

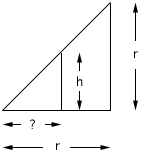
If you think of the hemisphere and the region between the cone and the cylinder in Figure 1 as being constructed of layers as in figure 2 then the volume of the hemisphere is equal to the volume of the region between the cone and the cylinder. The volume of the cylinder is pi*radius2*height = pi*r3. The volume of the cone is (1/3)*pi*radius2*height = (1/3)*pi*r3. Hence the volume of the hemisphere is pi*radius2*height = pi*r3 -  (1/3)*pi*r3 =  (2/3)*pi*r3 Thus the volume of the sphere of radius r is  (4/3)*pi*r3

There is a similar construction where Archimedes develops the expression for the surface area of a sphere. Walter and Chris showed this to me in the answer to an earlier question

I hope this helps,
Harley
Go to Math Central