|
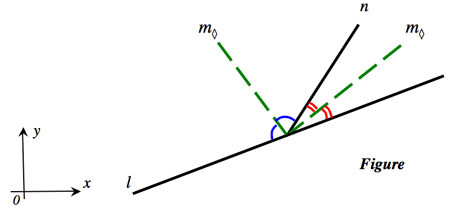
Consider two lines having slopes $l$ and $n$ on the Cartesian plane, see Figure below.Their angle bisectors, shown with dotted lines in the figure, have the slopes
\[ \frac{a}{b \pm \sqrt{a^2 + b^2}} \hspace{30 mm} \mbox{(i)}\]
where $a = l + n, b = 1 - nl$ . Expression (i) , denoted further $m_{\large \diamond}$, could be interpreted also as a diamond slopes.
It is easy to derive (i) as a corollary of the identity
\[\tan^{-1}l + \tan^{-1}n = 2 \tan^{-1}\frac{a}{b + \sqrt{a^2 + b^2}}\hspace{20 mm} \mbox{(ii)}\]
Indeed. The denominator of (i) has two cases, "+" and “−”. The "+" case is obviously equivalent to (ii), and the slope of the one angle bisector $\large \frac{a}{b + \sqrt{a^2 + b^2}}$ is immediately derived (the angle labled red in the figure). The “−” case leads to the other angle bisector (the angle labled blue in the figure), which is perpendicular to the first one, and therefore its slope (as a negative reciprocal of $\large \frac{a}{b + \sqrt{a^2 + b^2}}$) equals $\large \frac{a}{b - \sqrt{a^2 + b^2}}.$ Thus the slopes of the angle bisectors $m_{\large \diamond} = \large \frac{a}{b \pm \sqrt{a^2 + b^2}}.$ QED.
The relationship $m_{\large \diamond}$ can be used for finding slopes in various situations, especially ones related to symmetry. It formally generalizes the slope relationships $m_{\parallel} = m$ and $m_{\perp}= m^{-1}$ for parallel and perpendicular lines respectively. Students could benefit from learning a connected system of slope relationships, rather than “disjoint particles” $m_{\parallel}$ and $m_{\perp}.$
Special thanks to Yue Kwok Choy from Hong Kong for using our results (i) and (ii) in his note “Slope of angle bisectors of rhombus” (Questions 1, 2 and identity (3)) posted in 2012. The author attempted to derive (i) and (ii) there, but his proof was not complete. The reason for mentioning this is the following. The identity (ii) holds universally for any $l,n \in \mathbb{R}$ (in fact for any $l,n \in \mathbb{C}$) while the identity
\[\tan^{-1}l + \tan^{-1}n = \tan^{-1}\frac{a}{b} \hspace{20 mm} \mbox{(iii)}\]
which was used in the note “Slope of angle bisectors of rhombus”, is significantly restricted: it holds only if $b = 1 - nl > 0.$ For example, for $l = 1$ and $n = 2$ relationship (iii) is false. Therefore the domain of (iii) is a little too narrow for deriving (ii).
Alternatively to (i), the slopes of the angle bisectors $m_{\large \diamond}$ can be introduced as a solution of a quadratic equation:
\[ax^2 + 2bx - a = 0 \hspace{40 mm} \mbox{(iv)}\]
This approach extends students’ practice in setting eqations and applying the quadratic formula. To prove (iv) consider two cases. When $a = l + n = 0,$ then $b = 1 - ln = 1 + n^2 \ne 0.$ In this case $m_{\large \diamond} = 0$ and equation (iv) also has the only zero root. When $a \ne 0$ equation (iv) has two roots:
\[x_{1,2} = \frac{-b \pm \sqrt{a^2 + b^2}}{a} = \frac{a}{b \pm \sqrt{a^2 + b^2}} = m_{\large \diamond} \mbox{. Q.E.D}\]
Let’s illustrate it.
Example. If the line having the slope $m$ bisects the angle between the lines $x-y-8=0$ and $7x-y-12=0,$ find $m.$
Solution. The slopes of the given lines are $ l =1$ and $n = 7.$ Then $a = l + n = 8$ and $b = 1 - nl =-6.$ The quadratic eqation (iv) becomes $2x^2-3x-2=0.$ Its solution, $2$ or $\Large -\frac{1}{2}$, is the answer.
Either (i) or (iv) could be constructively considered and conceptually integrated as a regular component of high school program and its enrichment starting from Grades 10-11.
Copyright © May, 2012 by Gregory V. Akulov
|

