Loran is referred to as a hyperbolic system.  In order for the Loran system to work effectively, the Loran receiver must be connecting with at least three transmitting stations.  This set of three stations is called a chain.  One of these stations is designated as the master station and the other two are secondary stations.  Each station sends out repeated signals, traveling at the speed of light, pulsing at specific time intervals.  The chain of stations has unique time delays to distinguish chains from one another.  These signals reach the Loran receiver, located on the ship.  By analyzing these time delays, we are able to calculate the difference in distance from the ship to the master station and from the ship to one of the secondary stations.

The hyperbola has a very important distance property that helps locate the ship.  The hyperbola is the set of all points where the difference in distance to each of the foci of the hyperbola is constant.  This special property is the foundation for Loran.

We can imagine that the world is flat and that the coverage area of a chain can be shown on a Cartesian plane.  The master station and two secondary stations are plotted on the grid.  To find the location of the Loran receiver, presumably on a ship, we need to find the difference in distance from each master/secondary pair to the ship.  The ship will be somewhere in the coverage area of a chain (illustrated on the grid).  Using the time delays as they reach the receiver on the ship, we are able to calculate the difference in the distance from the ship to each master/secondary pair, as well as which station the ship is closer to, the master or the secondary.  These distances can be converted to longitude and latitude coordinates and the master/secondary pair becomes the foci of a hyperbola.  These particular foci generate several different hyperbolas.  Because of the special distance property, we can find which hyperbola has a difference of distance that coincides with the constant our receiver calculated.  Somewhere on this hyperbola will be the ship. 

This same process is repeated for the other secondary station and the master station.  Where the two corresponding hyperbolas meet is the location of the ship.  Because we are able to find which stations the ship is closest to, there is only one possible location for the ship.

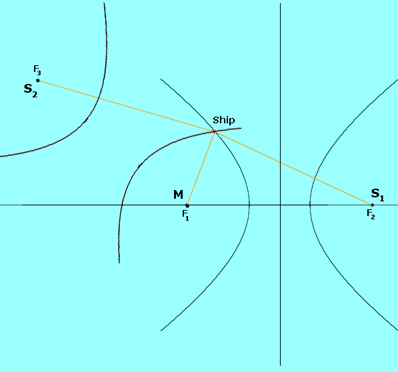
In the picture above, M and S₁ are the focal points of one hyperbola. M and S₂ are the focal points of the second hyperbola. Where these hyperbola meet is the location of the ship.