Natasha Glydon

Two conic sections, the hyperbola and the circle, have inspired two very useful navigational systems.  One, known as Loran (Long Range Navigation) was first used during World War II, in the early 1940’s.  Loran uses hyperbolic branches and chains of stations to aid ships and aircrafts in navigation.  The second is the global positioning system or GPS.  GPS uses satellites and circles to locate a receiver anywhere in the world.  GPS was fully functional in July of 1995 and did become a more versatile alternative to Loran, however, Loran is still in use today as a support for the new global positioning position.

The Mathematics of Loran

Loran is referred to as a hyperbolic system.  In order for the Loran system to work effectively, the Loran receiver must be connecting with at least three transmitting stations.  This set of three stations is called a chain.  One of these stations is designated as the master station and the other two are secondary stations.  Each station sends out repeated signals, traveling at the speed of light, pulsing at specific time intervals.  The chain of stations has unique time delays to distinguish chains from one another.  These signals reach the Loran receiver, located on the ship.  By analyzing these time delays, we are able to calculate the difference in distance from the ship to the master station and from the ship to one of the secondary stations.

The hyperbola has a very important distance property that helps locate the ship.  The hyperbola is the set of all points where the difference in distance to each of the foci of the hyperbola is constant.  This special property is the foundation for Loran.

We can imagine that the world is flat and that the coverage area of a chain can be shown on a Cartesian plane.  The master station and two secondary stations are plotted on the grid.  To find the location of the Loran receiver, presumably on a ship, we need to find the difference in distance from each master/secondary pair to the ship.  The ship will be somewhere in the coverage area of a chain (illustrated on the grid).  Using the time delays as they reach the receiver on the ship, we are able to calculate the difference in the distance from the ship to each master/secondary pair, as well as which station the ship is closer to, the master or the secondary.  These distances can be converted to longitude and latitude coordinates and the master/secondary pair becomes the foci of a hyperbola.  These particular foci generate several different hyperbolas.  Because of the special distance property, we can find which hyperbola has a difference of distance that coincides with the constant our receiver calculated.  Somewhere on this hyperbola will be the ship. 

This same process is repeated for the other secondary station and the master station.  Where the two corresponding hyperbolas meet is the location of the ship.  Because we are able to find which stations the ship is closest to, there is only one possible location for the ship.

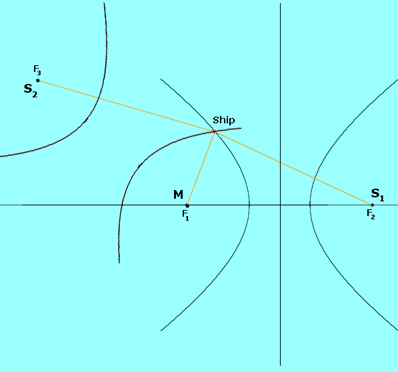
In the picture above, M and S₁ are the focal points of one hyperbola. M and S₂ are the focal points of the second hyperbola. Where these hyperbola meet is the location of the ship.

GPS and Circles

Similar to the Loran system, GPS works successfully with the transmission of signals, traveling at the speed of light.  In the case of GPS, we are working with satellites instead of stations.GPD uses twenty-four satellites that orbit the entire earth, and hence it can provide important navigational information anywhere in the world.  

Also similar to the Loran, three satellites are needed to find the altitude, longitude, and latitude of a GPS receiver on earth.  The satellites send signals that are picked up by the GPS receivers, just like the Loran system.  The receiver is then able to find the distance from each of the three satellites to the receiver. Because we know how fast the signals are traveling (the speed of light), the simple distance formula provides us with this information (distance = speed x time ).  Instead of using the hyperbola, each of the three satellites becomes the centre for a sphere; with a radius equal to the distance we calculated using the formula.  The three spheres will intersect at two points, one of which is usually unrealistic, perhaps below sea level.  If there are two plausible points, a fourth satellite distance calculation may be needed.  The appropriate point of intersection is the location of the receiver.  The process of using three (or more) spheres to locate a point is called trilateration.

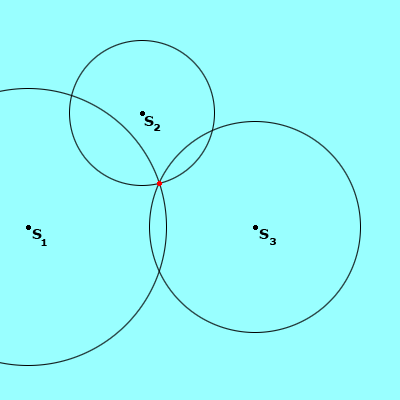
The picture above shows three circles of varying distances, centered around satellites (S₁ , S₂ , and S₃ ). The point where the three circles (or spheres, as is the case with GPS) meet is the location of the GPS receiver.

GPS and the Loran system are built on the foundation of fairly common mathematical concepts – conic sections and distance formulas.  Although the actual mathematics involved requires rather complex calculations, it is helpful to understand, even broadly, how these systems work.  Of course, the receivers now do much of the mathematics involved, but it is interesting to see how practical conic sections can be.