The Arc Midpoint Find

To continue on the topic of circular arc midpoint computation, consider the following proposition which is valid in $\mathbb{R}^n$.

Let $AMB$ be an arc (see figure) with center C, midpoint M, and angular measure $2\theta \ne \pi$. If points M, C, A and B have $x$-coordinates $\mu$, $c$, $2a$, and $2b$ respectively, then

\[\mu = c + (a + b - c)\sec\theta\]

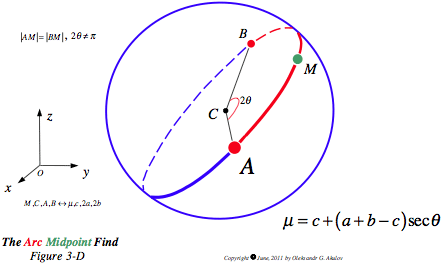
The same holds for the other $n-1$ coordinates $y, z, ... w$.
Below we present two different approaches to the proof of the proposition.

First approach:

As discussed in Dot Product Finds Arc Midpoint, $M$ obeys the vector equality $\vec{OM} = \vec{OC} \pm \left( \vec{CA} + \vec{CB} \right)/(2\lambda)^{1/2}$, where $\lambda = 1+\left( \vec{CA} \cdot \vec{CB}\right)/r^2 = 1 + \cos2\theta$, $r$ is a radius of the arc. Hence, without loss of generatlity, $x$-coordinates satisfy $\large \mu = c \pm \frac{(2a-c) + (2b-c)}{\sqrt{2(1+\cos2\theta)}} = c + (a + b - c)\sec\theta$

Second approach:

Let $T$, with $x=t$, be the midpoint of the chord $AB$. Denote $|CT|=h$. Then, without loss of generaliry, $|t-c|:|\mu - c|=h:r$. Since $h:r=|\cos\theta|$, and $t = a+b$, we get $|\mu - c|=|a+b-c||\sec\theta|$, which obviously holds with no modulus as well. So, $\mu = c + (a + b - c)\sec\theta$

What if $2\theta = \pi$? In that case infinitely many different values of $\mu$ can be found.

Copyright © August, 2011 by Oleksandr G. Akulov