Hi George,

I drew a diagram of what you described and let the side length be $s$ feet and the diameter of the octagon be $d = 2 \times 16 + 2 \times 1 = 34$ feet.

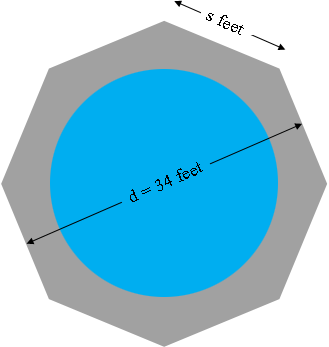
I then used an expression in my response to an earlier question that related $s$ to $d.$

\[s = \frac{d}{1 + \sqrt2} = \frac{34}{1 + \sqrt2} = 14.08 \mbox{ feet.}\]

I then used an expression from Stephen's response to another question to find the surface area $A$ of the octagon

\[A = \frac{s^2 n}{4 \tan\left(\frac{360^o}{2 n}\right)}\]

where $n$ is the number of sides of the polygon, in your case $n = 8.$ (Notice that I changed the notation since Stephen used $a$ for the side length.) For your octagon I get the surface area to be

\[A = \frac{14.08^2\times 8}{4 \tan\left(\frac{360^o}{16}\right)} = 957.66 \mbox{ square feet.}\]

You probably also want to know the number of cubic yards of concrete you will need. First divide 957.66 by 9 to convert the area to square yards. Divide the thickness of the concrete, measured in inches, by 36 to convert the thickness to yards. Finally multiply the area in square yards by the thickness in yards to obtain the volume of concrete in cubic yards.

Penny