Hi Joel,

I can try to help but I need to know about your mathematical background. Do you know about similar triangles?

Penny

Joel wrote back

By similar, do you mean same angles but different sizes?

Yes. If measures of the angles of one triangle are equal to the measures of the angles of another triangle then the triangles are said to be similar. Trigonometry is based on similar triangles so I want to spend a few minutes on similar triangles.

In my diagram below the Two triangles ABC and ADE are similar. I am going to use |AB| as the length of the line segment AB, |BC| as the length of the line segment BC and so on.

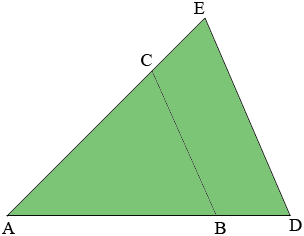
A very useful fact about similar triangles is illustrated in this diagram. I drew it so that the length of AB is three-quarters the length of AD, then because the triangles are similar the length of AC is three-quarters the length of AE and the length of BC is three-quarters the length of DE. Thus

\[\frac{|AB|}{|AD|} = \frac{|AC|}{|AE|} = \frac{|BC|}{|DE|} = \frac{3}{4}.\]

In general we can say that the lengths of corresponding sides of similar triangles are in proportion.

Hence if triangles ABC and PQR in the diagram below are similar

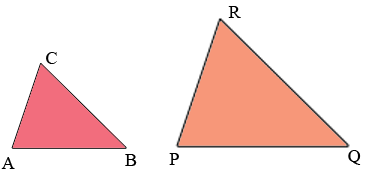
then

\[\frac{|AB|}{|PQ|} = \frac{|AC|}{|PR|} = \frac{|BC|}{|QR|}.\]

Here are three questions we have received concerning similar triangles. Have a look and see if you can solve them or if you understand our solutions.. Again since I am not sure of your background there may be concepts here that are new to you. If so don't hesitate to ask. Once I am sure you are comfortable with similar triangles we will move on to trigonometry.

http://mathcentral.uregina.ca/QQ/database/QQ.09.06/h/vivienne1.html

http://mathcentral.uregina.ca/QQ/database/QQ.09.08/h/jane2.html

http://mathcentral.uregina.ca/QQ/database/QQ.09.07/h/krista1.html

Penny