Hi Reuben,

I drew a diagram of your plot (not to scale) and added a line from $B$ to $D.$

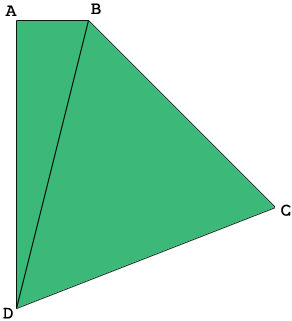
Since the angle at $A$ is a right angle I can use Pythagoras Theorem to find that the length of $BD,$ which I call $LBD$ is 213.42 meters. This way your plot is partitioned into two triangles and I know the lengths of the sides of the triangles so I can find the areas of the triangles using Heron's Formula. Heron's Formula gives the area in square meters s I divided by 4046.86 to convert it to acres. My calculations gave the area of your plot as 5.5 acres. I also used the Law of Sines and the Law of Cosines to determine the measures of the angles in these triangles. Finally I put the coordinate system on the plane with $A$ at the origin, the B on the X-axis and $D$ on the negative Y-axis. This allowed me to find the coordinated of $A, B, C,$ and $D$ and the slope of the line $CD.$

You want to subdivide your plot by lines parallel to $CD$ so I let $P$ be a point on the line $DA, k$ meters from $D,$ and $R$ be a point on $DA, h$ meters From $P.$ The lines $PQ$ and $RS$ are parallel to $CD.$

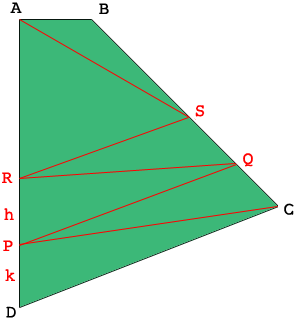
The lines $PC, RQ$ and $AS$ subdivide the quadrilaterals $CDPQ, QPRS$ and $SRAB$ into triangles so I can use Heron's Formula again to calculate the areas.

The image below is a screen shot of the Microsoft Excel file I used to make the calculations.

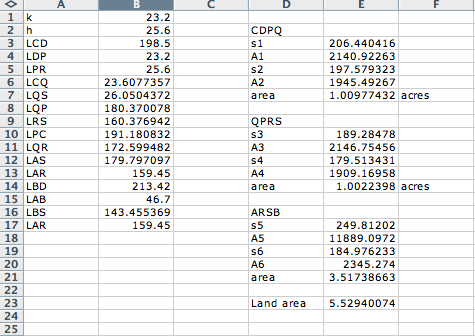
The side lengths are proceeded with an $L,$ for example the length of $CD$ is $LCD.$ The entries in columns D and E are area calculations using Heron's Formula. Hence when $k = 23.2$ meters and $h = 25.6$ meters the two plots $CDPQ$ and $PQRS$ are 1 acre each and the remaining portion, $ARSB$ is 3.5 acres.

I have attached the spreadsheet so you can modify the calculations if you wish. Download the spreadsheet. To use the spreadsheet set $h$ (entry B2) to be some small number, say $h = 10$ meters and modify $k$ until the area of $CDPQ$ is what you desire. Leaving $k$ unchanged modify $h$ until the area of $QPRS$ is what you desire.

I hope this is some use to you. Write back if my instructions are not clear.

Harley