Obviously, architecture is geometric – a clear link to mathematics. Buildings, bridges, furniture, vehicles, they all have unique shapes. It is easy to see how this broad definition of architecture is related to math. However, the mathematics behind architecture is far more than just shapes. To think of an architect in general, much of their job is focused on math. Consider blue prints for example. A blue print is the paper layout, drafted by an architect, which illustrates the design of a building. Blue prints are drawn to scale, enabling the designer and the consumer to accurately envision what the building will look like in terms of size and space. Math also provides architects with a solution to the question of possibility. Think of yourself as an architect. In your mind, you dream up a beautiful building; you can actually picture it in your head. But how does that dream building become a blue print; become an actual structure? Math enables architects to make their dreams possible by providing a guarantee for adequate heights, weights, and angles for various structures, to ensure safety and cost efficiency. Are their ideas and visions really plausible? Math provides the answer.
Everyday Math Problems
It is not only architects who design and build practical structures. Everyday people commonly do construction work to their houses and yards. It would be very expensive to hire an architect if you just wanted to build a fence or a new deck. Luckily, the basis of successful construction and architecture is math. For example, imagine you are redecorating your living room. You want to hang three pictures on the wall in a triangular shape. You realize that you must put the nails in the vertices of an equiangular triangle in order to create the shape you want. However, the studs in the wall are spaced 40cm apart. How will you arrange the pictures so that the nails are in the studs and still forming an equiangular triangle? If each of the three pictures is a square of measurement 20cm by 20 cm, does your solution work? How do you know?
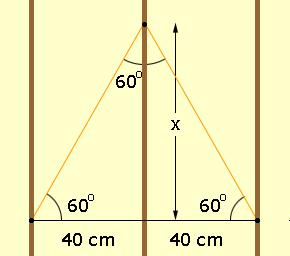
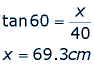
We can look at our solution and its plausibility from an architectural perspective. By placing the nails in the studs, we know that the pictures will be supported enough not to fall from the wall. There are several possible solutions, but we want our pictures as close together as possible to maximize wall space. If the pictures are 20cm x 20cm, we can see that our solution is possible. By making sure that our solution works, we do not hammer unnecessary holes into the wall, like we might by using trial and error.
You may also want to take a look at some other architectural math problems encountered by everyday people, which were sent in to Math Central:
Angles in a hexagon
Building a poker table
Hauling dirt
Framing
Building a deck
Building a wishing well
Check out the website for more examples.
Symmetry
Natasha Glydon
Commonly, we consider symmetry to include basic line symmetry only. We think of the human body, maybe a lamp, or something else that is vertically symmetrical. But symmetry includes much more than just line symmetry. Symmetry includes patterns and explaining repetition in design.
Architecture encompasses other types of symmetry as well, including: rotational (the Pentagon), spiral (spiral staircases), cylindrical (the Calgary Tower), chiral (human hands), similarity (the roof of a pagoda), and translational (repetition) symmetry. Ultimately, symmetry is a way to describe shapes and design and to organize geometry.
 |
One architectural feature where symmetry is evident is a frieze design. A frieze design consists of repeated copies, along a line, of a single figure or block. If we categorize frieze designs by the amount of symmetry they have there are seven symmetry groups. Frieze patterns can be seen on walls, railings, verandahs, etc. These patterns can be seen in art and architecture around the world. The transformations that produce these symmetries are very common to the mathematical world. For more information on frieze patterns, visit the Math Central website and enter the word frieze into the resource room research window.
In modern types of architecture, it sometimes seems impossible to recognize a pattern. When patterns seem completely random, like the weather, for example, Chaos Theory can explain the hidden patterns. Chaos Theory is built on the basis of the Butterfly Effect. Essentially, even the smallest initial change can make the end result substantially different. Chaos Theory is most commonly used to predict weather conditions and guess future population numbers. However, the seeming randomness of chaos is what defines modern architecture.
Suspension Bridges
Natasha Glydon
Building bridges is a common job for many architects. Aside from the geometric shapes of the bridges themselves, architects are also responsible for the engineering of safety features as well. As is the case with bridges, architects need to consider the length of the bridge, the weight it can withstand, weather conditions, etc. Different bridge structures are used for different purposes. One of the most common and mathematically interesting bridge types is the suspension bridge. Suspension bridges are useful because they can be quite long and still work effectively.
 Image reproduced with permission of Brooklyn Bridge Gallery |
In a suspension bridge, the roadway is actually hanging from large cables. The cables run over the top of two large towers (which are rooted deep into the earth) and connect to anchorages at each end of the bridge. When constructing a bridge, architects must consider the compression and tension forces that the bridge is going to have to withstand – compression and tension. Consider a long piece of wood resting on two crates. As you put weight onto the middle of the wood, the top part of the wood shortens while the underside of the piece lengthens, making the middle sag and the ends lift up. This is because compression forces are shortening the top part of the wood and tension forces are elongating the underside of the wood.
The cables and the towers of the suspension bridge are designed to deal with the weight of traffic. The towers are dug deep into the earth for stability and strength. Tension is combated by the cables, which are stretched over the towers and held by the anchorages at each end of the bridge. Wind can be detrimental to a bridge. For that reason, a deck truss is often placed under the roadway of the bridge. This provides additional stability for the bridge.
The parabolic shape of the suspension bridge is also interesting. At first glance, the curve may be described as a catenary. A catenary is a curve created by gravity, like holding the end of a skipping rope in each hand and letting it dangle. However, because the curve on a suspension bridge is not created by gravity alone (the forces of compression and tension are acting on it) it cannot be considered a catenary, but rather a parabola. The parabolic shape allows for the forces of compression to be transferred to the towers, which upholds the weight of the traffic. The parabolic shape can also be proved mathematically, using formula comparisons.
Many avenues of architecture, construction, and design use math to create a variety of pieces. Math aids developers by providing proof that something is possible and also defines shapes and designs. We can use numbers to describe a design or a construction. In this way, math has a significant effect on architecture.
