Solution to December 2005 Problem

The Problem:
The hands on my watch turn in a continuous motion. At the precise instant when the second hand passes one of the 12 subdivisions of the face, I know that in less than half-a-second the minute hand will pass precisely over the hour hand. At what time will this occur, if it takes place before noon?

            We received correct solutions from

Solution.

The hour hand and the minute hand each moves at a constant rate, so there is a fixed interval between the times at which they point in the same direction.  The minute hand passes over the hour hand precisely at midnight, and they coincide 11 times during the next twelve hours.  This means that they coincide every 12/11 hours; in other words, the fixed interval from one crossing to the next is

1 hour, 5 minutes, 27 and ³/₁₁ seconds.

(As a quick check, note that as the minute hand goes 1 and ¹/₁₁ times around, the hour hand moves ¹/₁₁ of the way around.)  The two hands thus coincide at 1:05:(27+ ³/₁₁), and again exactly one hour, five minutes, and 27+ ³/₁₁ seconds later at 2:10:(54+ ⁶/₁₁), and so on.  We thus arrive at the list of times when the minute hand crosses over the hour hand:

The second hand has passed over one of the face's 12 subdivisions when the whole number of seconds is divisible by 5: at 7:38:10 (coincidence of the hour and minute hands occurs 10/11 seconds later) and at 9:49:05 (coincidence occurs 5/11 seconds later).  Since 5/11 is less than half a second, the crossing we seek occurs less than a half second before 9:49:05 each morning.

            All solvers provided a variation of the preceding argument.  In addition Kais gave a second argument that avoided making a list of possibilities.  Note that the nth coincidence of the hands occurs ¹²/₁₁ 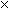3600 n  seconds after midnight, and that

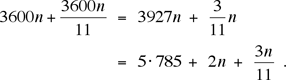
We are interested in those values of n for which