| PM87: May 2009 |
 |
Our goal this month is to correct a flaw in the usual ordering of the positive integers: when n is odd then it divides 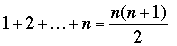 but when n is even then it does not divide 1 + 2 + ... + n; so it is only half the time that the nth integer divides the sum of all the integers up to it. Our problem is to find a better ordering of the positive integers; specifically, but when n is even then it does not divide 1 + 2 + ... + n; so it is only half the time that the nth integer divides the sum of all the integers up to it. Our problem is to find a better ordering of the positive integers; specifically,
find a sequence a1, a2, a3, ... of positive integers such that
(i) every positive integer appears exactly once in the sequence, and
(ii) for every n, an divides a1 + a2 + ... + an.
|
 Solution. Solution.
|
| PM86: April 2009 |
 |
Find integers a and b such that neither 7 nor 18 divides ab(a+b),
while 77 does divide (a+b)7-a7-b7.
|
 Solution. Solution.
|
| PM85: March 2009 |
 |
A polyhedron with six edges is called a tetrahedron, and a polyhedron with eight edges is called a quadrangular pyramid. What is a polyhedron with seven edges called?
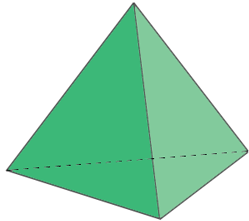
Tetrahedron
6 edges |
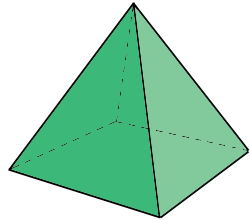
Quadrangular Pyramid
8 edges |
Background. For our purposes, a polyhedron is a solid figure bounded by polygonal faces. Each of its edges joins two vertices and is a common side of two adjacent faces. A vertex is a point where three or more edges meet, and it forms a corner where three or more faces come together.
|
 Solution. Solution.
|
| PM84: February 2009 |
 |
-
Find a 6-digit number that is multiplied by a factor of 6 if the final three digits are removed and placed (without changing their order) at the beginning; specifically, if we write the integer in terms of its base-10 digits as abcdef, then
6 × abcdef = defabc.
- Can you do the analogous thing with an 8-digit number? That is, can you find an 8-digit number that is multiplied by a factor of 6 when the final four digits are removed and placed (without changing their order) at the beginning?
|
 Solution. Solution.
|
| PM83: January 2009 |
 |
Let a0 = 2009 and 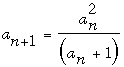 for any non-negative integer n. Prove that 2009 – n is the greatest integer less than or equal to an for 0 ≤ n ≤ 1005. for any non-negative integer n. Prove that 2009 – n is the greatest integer less than or equal to an for 0 ≤ n ≤ 1005.
|
 Solution. Solution.
|
| PM82: December 2008 |
 |
A point is placed inside an equilateral triangle so that its distances from the three vertices are 5, 12, and 13. Find the area of the triangle.
|
 Solution. Solution.
|
| PM81: November 2008 |
 |
For which k ≥ 3 is a 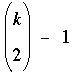 prime power pn? prime power pn?
|
 Solution. Solution.
|
| PM80: Octobr 2008 |
 |
Find the longest sequence of real numbers such that the sum of every 7 consecutive terms is positive while the sum of every 11 consecutive terms is negative.
|
 Solution. Solution.
|
| PM79: September 2008 |
 |
The 1990 TV movie Gunsmoke: The Last Apache added an interesting twist to the traditional duel: Six shot glasses of whiskey were set on the bar; in one of them was a lethal dose of strychnine. The duelists took turns emptying the glasses with the good guy drinking first. He survived and laughed triumphantly, "Ha, you should have gone first. The first man to drink had a numerical advantage!"
Our question: What do you think about the scriptwriter's mathematical aptitude? More generally, in a duel with n glasses, with just one containing the deadly poison, the two participants take turns emptying the glasses, one at a time, until one drops dead from the poison. What is the probability that the one who drinks first is the one to die?
|
 Solution. Solution.
|

