MP60: May 2006

Find the greatest common divisor of the 1003 integers

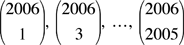
where 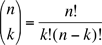is the number collections of k objects that can be formed from a set of n objects.

Solution to May 2006 problem

MP59: April 2006

Two players take turns choosing a coefficient a_i from the polynomial

x¹⁰ + a₉ x⁹ + ... + a₁ x + 1

and replacing it with an arbitrary real number. The game ends after 9 moves, when the values of all nine a_i's have been selected. The first player to choose wins the game if the resulting polynomial has no real root, while the second player wins if the polynomial has at least one real root. One of the players has a winning strategy -- he wins no matter what his opponent does. Which player is it, and what is his winning strategy?

Solution to April 2006 problem

MP58: March 2006

Our March problem comes from a recent math contest.

John writes a number with 2187 digits on the blackboard, each digit being a 1 or a 2. Judith creates a new number from John's number by reading his number from left to right and wherever she sees a 1 writing 112 and wherever she sees a 2 writing 111. (For example, if John's number begins 2112, then Judith's number would begin 111112112111.) After Judith finishes writing her number, she notices that the leftmost 2187 digits in her number and in John's number are the same. How many times do five 1's occur consecutively in John's number?

 

Solution to March 2006 problem

We are given a pair of quadratic equations with integer coefficients b and c,

x²– bx + c = 0  and  x²– bx – c = 0,

and call them a compatible pair if they both have integer solutions.  For example,

            x²– 5x + 6 = 0 has solutions 2 and 3, while

            x²– 5x – 6 = 0 has solutions –1 and 6.

Of course, we can multiply b and c by d and d² to get a related compatible pair x²– bdx ± cd² = 0, but we are interested in pairs where b and c have no common divisor.  Are there any other compatible pairs?

This month's problem is based on an interesting result of Jeffrey L. Poet and Donald L. Vestal, Jr.  We will give you the complete reference next month.

Solution to February 2006 problem

MP56: January 2006

Greetings for the new year. The Monthly Problem team wishes you all the health and happiness this coming year as you enjoyed last year:

Find the maximum value of f(2006) - f(2005) where f is a real valued function that satisfies the inequality 

|f(x) - f(y)| ≤ (x-y)²

for all real numbers x and y

Solution to January 2006 problem

MP55: December 2005

The hands on my watch turn in a continuous motion. At the precise instant when the second hand passes one of the 12 subdivisions of the face, I know that in less than half-a-second the minute hand will pass precisely over the hour hand. At what time will this occur, if it takes place before noon?

Solution to December 2005 problem

MP54: November 2005

Professor Adams wrote on the blackboard a polynomial, f(x), with integral coefficients and said, "Today is my son's birthday, and when we substitute his age A for x, then f(A) = A. You will also note that f(0) = p, and that p is a prime number greater than A." How old is Professor Adams' son?

Solution to November 2005 problem

The first player tosses a coin 1001 times while the second player tosses a coin only 1000 times. What is the probability that the first player gets more heads?

(Please avoid tedious computations here.)

Solution to October 2005 problem

MP52: September 2005

Our first problem of the new season deals with integers.  As a warm-up exercise after the long summer break you might try to show that for every odd number n, 4ⁿ + 1 is a multiple of 5. For the September problem you must:

Prove that if the number n is odd and greater than 3
then 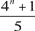 cannot be a prime number.

Solution to September 2005 problem