|
Solution to March 2006 Problem
John writes a number with 2187 digits on the blackboard, each digit being a 1 or a 2. Judith creates a new number from John's number by reading his number from left to right and wherever she sees a 1 writing 112 and wherever she sees a 2 writing 111. (For example, if John's number begins 2112, then Judith's number would begin 111112112111.) After Judith finishes writing her number, she notices that the leftmost 2187 digits in her number and in John's number are the same. How many times do five 1's occur consecutively in John's number?
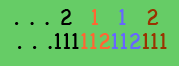
In mid-February each year, students from grades 9 to 11 across Canada write the University of Waterloo's math contests. Our problem this month was the final question from last month's Pascal Contest (for grade 9s).
We received correct solutions from
Vincent Bardoux (France) |
|
Wolfgang Kais (Germany) |
Mohamed Benchaib (Marocco) |
|
Karim Laaouini (Morocco) |
Pierre Bornsztein (France) |
|
Normand LaLiberté (Ontario) |
Bernard Carpentier (France) |
|
Matthew Lim (internet) |
| K.A. Chandrashekara |
|
Juan Mir Pieras (Spain) |
| Philippe Fondanaiche (France) |
|
Mark Pilloff (USA) |
| Xavier Hecquet (France) |
|
A. Teitelman (Israel) |
| LeCarré de l'Hypoténuse (France) |
|
Said Amghibech (internet) |
Solution.
There are 182 strings of five consecutive 1s in John's number.
Most solutions came to this conclusion through a similar sequence of simple observations.
Observation 1. Judith's sequence must begin with either 111 or 112; since her initial digits are the same as with John's, we see that the numbers of both John and Judith must start with 1 (reading the numbers from left to right).
Observation 2. John's number is completely determined: since its first digit is 1, Judith's first three digits are 112. Because these are also John's first three digits, the number must begin
112 112 111
(after Judith replaces, in turn, the 1, 1, and 2). We continue the process in stages: Judith replaces the first 3k digits of John's number to obtain the first 3k+1 digits of her number, which then must be the first 3k+1 digits of John's number.
Observation 3. The rules imply that the number of 2s in the k+1st stage equals the number of 1s in the kst stage. Moreover, there can never be consecutive 2s because any 2 would come at the end of a triple, to be followed by the next triple that begins 11. A string of five consecutive 1s in stage 3k+1 thus comes from the sequence 21 in stage 3k. It follows that the number of these 5-strings (which we wish to count) equals the number of pairs 21 in the previous stage.
The process is now clear: at each stage we count the number of 1s and 2s; that gives us the number of 2s and 5-strings, respectively, in the succeeding stage. Almost. There is one small technicality: If the digit 2 appears at the end of the sequence at the kth stage, the sequence in the k+1th stage would end with a block of three 1s, not five. Thus, the actual number of 5-strings in any stage equals one less than the number of 2s in the previous stage should that stage end with a 2. To be more precise, the generating rule states that the final digit at an odd-numbered stage is 1, and at an even numbered stage is 2. Thus, the number of 5-strings in stages 1, 3, 5, and 7 equals the number of 2s in stages 0, 2, 4, and 6; the number of 5-strings in stages 2, 4, and 6 equals one less than the number of 2s in the previous stages.
In the following table the number of digits observed in John's sequence is 3k where k is the current stage. The number of 1s is the number of digits in that stage less the number of 1s in the previous stage; that is because the number of 2s in the sequence equals the number of 1s in the previous stage. The number of 5-strings essentially equals the number of 2s in the previous stage. The question calls for the number of 5-strings in the 7th stage, which the table establishes to be 182.
Stage |
# digits observed |
#1s |
#2s |
#5-strings |
0 |
1 |
1 |
0 |
0 |
1 |
3 |
3 – 1 = 2 |
1 |
0 |
2 |
32 = 9 |
9 – 2 = 7 |
2 |
1 – 1 |
3 |
33 = 27 |
27 – 7 = 20 |
7 |
2 |
4 |
34 = 81 |
81 – 20 = 61 |
20 |
7 – 1 |
5 |
35 = 243 |
243 – 61 = 182 |
61 |
20 |
6 |
36 = 729 |
(547) |
182 |
61 – 1 |
7 |
37 = 2187 |
(1640) |
(547) |
182 |
Further comments.
Many correspondents found this month's problem fascinating. They noted that the rule for generating the sequence allows the process to continue forever, so they provided an analysis of the number of 1s and 2s at stage 3n for all n > 0. The number of 1s is, from the third column of our table,
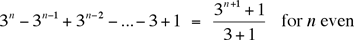
and
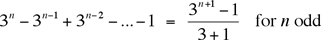
Thus, the first 3n digits of the sequence will consist of 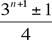 ones and ones and 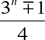 twos. So, for example, when n = 5 — an odd number — there are (36 – 1)/4 = 728/4 = 182 ones. As a consequence, there will be 182 twos among the first 36 = 729 digits, and (since 6 is even) the 729th digit is a 2, so we have confirmed that the number of 5-strings among the first 37 = 2187 digits is indeed 182. twos. So, for example, when n = 5 — an odd number — there are (36 – 1)/4 = 728/4 = 182 ones. As a consequence, there will be 182 twos among the first 36 = 729 digits, and (since 6 is even) the 729th digit is a 2, so we have confirmed that the number of 5-strings among the first 37 = 2187 digits is indeed 182.
The rule for rewriting the John's sequence has an interesting consequence. If at stage k we denote by A and by B the initial and final blocks of 3k-1 digits, then that string of 3k digits has the form AAB, while the next stage has the form AAB AAB AAA (just as we saw in going from 112 to 112 112 111). Furthermore, as we have just seen, the number of 2s at each stage is within one of ¼ of the digits. Even though the sequence consists of such regular patterns, Mir observed that the infinite sequence could not be periodic for any finite period — should a string of p digits starting at digit d end in a 1, the corresponding string in the rewritten sequence (of 3p digits starting at digit 3d) would end in a 2, and vice versa, were it to end in a 2, the rewritten sequence would end in a 1. Mir wondered whether there could be nice rules for rewriting sequences of 1s and 2s that would lead to infinite periodic sequences. Among his examples he suggested the rule to replace 1 by 121, and replace 2 by 212.
Finally, Hecquet provided John's number for the benefit of those who would like to see all 2187 digits.
John's number:
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112
112112111112112111112112112 |
| 
