|
|
|
Math Central - mathcentral.uregina.ca |
 |
 |
Problem of the Month 2007-2008
|
 |
 |
 |
 |
| PM79 Summer 2008 |
 |
Problem for Summer 2008
Instead of a monthly problem we offer you, for your enjoyment, a summer puzzle in the form of a sequel to Charles Perrault's classic tale "Le petit poucet" (translated into English as "Hop o' My Thumb"); the original is available for downloading from the Gutenberg Project in French or in English: http://www.gutenberg.org/browse/authors/p#a7137. Please send us your solution only if you can PROVE that it is the UNIQUE solution that will save the brothers. The solution will be published at the beginning of September.
The reading of the will was an occasion for the seven brothers to gather once again and reminisce about their childhood. Some memories were pleasant, but others were terrible and painful. There was the time when their parents had tried to lose them in the forest, and they had found their way again only because of the pebbles that the youngest had dropped along the way. Another time they had to run from a frightful ogre.
Now their parents had passed on, and predictably the seven brothers inherited the little old house in the woods where they had been born. However the testament also revealed a considerable surprise: Under the coal bucket in the cellar they were to find the key to the old chest sitting just beside it. Inside the chest they were to find the treasure that their parents had been saving for them.
So the seven brothers went to the cellar of the old house. The oldest lifted the coal bucket, and just then a clanking sound was heard, and a door slammed shut behind them. It was a heavy safe door with a strange combination lock of nine number dials arranged in a 3 by 3 square. They were trapped in the cellar. Nonetheless, the key was indeed under the bucket. When they opened the chest, a rat jumped out, and the brothers discovered that it contained only a short letter and a scrap of newspaper that the rat had been nibbling on. The letter was the last message from their parents:

The brothers frantically went back to the chest. They retrieved the scrap of paper, and to their dismay they discovered that the rat had chewed off the bottom left corner of the sudoku puzzle which was now their only chance of survival.
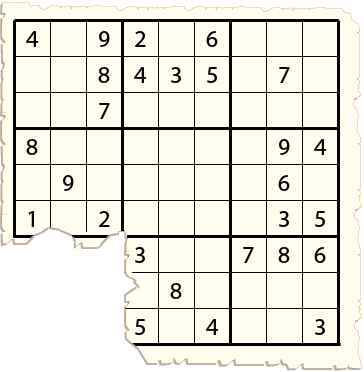
Fortunately, they were all of them avid sudoku players. They copied the puzzle sevenfold, in the hope that at least one of them would still find the solution. Then they started to work on it. The youngest brother had always been the quickest, but on this occasion he was remarkably slow. He would write down a few numbers, then pause for long meditations, while his older siblings scribbled frantically. Indeed in a matter of minutes, the six put down their pens and shouted "I've got it''. But then they compared their solutions, and found out that they were all considerably different. All solutions had the digits 1 through 9 appearing exactly once in every row, column and three by three square, but with the bottom left corner eaten by the rat, there was no way to tell which of their solutions was the correct one, if indeed any one was. At that point they felt sure that they were doomed and started to cry.
But then the youngest brother asked them to give him a little more time to concentrate, so he could find the correct solution. So for a few agonizing minutes, they watched him stare at the puzzle, tap his fingers, stare at the wall and write down a few numbers. When at last he produced his solution, the older brothers found that it was different from all of theirs. They could not tell why his solution was any better than any of theirs. But, he was the youngest, he was the brightest, they had trusted his judgment many times and, indeed, they had survived their childhood mostly because of that. So they set the number dials on the door to match the middle 3 by 3 square in the youngest's solution, pulled the handle and ···
Dear readers, we break off our story here and wish you a pleasant summer. We will post the ending in September. If you can guess how the story ends, you can send us, at The Problem of the Month, your ending with a complete justification.
|
 Solution. Solution.
|
| PM78: May 2008 |
 |
For which positive integers n can n! be written as a difference of two squares?
|
 Solution. Solution.
|
| PM77: April 2008 |
 |
Let a, b and c be positive integers whose only common divisor is 1 — that is, no integer greater than one divides all three — for which
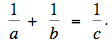
Prove that (a + b), (a – c) and (b – c) are all perfect squares.
|
 Solution. Solution.
|
| PM76: March 2008 |
 |
Four students, Adam, Barbara, Clara, and Dan, will win a prize if all of them succeed in their task:
One by one they will be taken into a room where there are four curtains, numbered one to four. The letters from A to D are written on four cards -- each letter on one and only one card -- and the cards are placed at random behind the curtains, one card behind each curtain. Each student will be allowed to look behind two curtains of his choosing. A student who finds a card with the first letter of his name behind one of his two chosen curtains succeeds. If all four students succeed, the group wins. If one or more does not succeed, the group loses.
The students are allowed to agree on a strategy together before the first is taken into the room. However, once a student has been in the room, no further communication is permitted, either by words or by signal. Additionally, students who have not been in the room have no way of knowing whether pervious students were successful or not.
If each student looks behind two curtains at random, each has a probability of 50% of succeeding, and the group would have a 6.25% probability of winning. Your challenge is to devise a strategy to give the group a probability of over 40% of winning. Please justify any your claims.
|
 Solution. Solution.
|
| PM75: February 2008 |
 |

A vertical plane contains a circle and point P: P lies outside the circle and above the horizontal line that the circle sits on. Your job is to stretch a thin wire in a straight line from P to a point Q on the circle so that a bead sliding down the wire will reach the circle in the least possible time. Gravity is the only force acting on the bead. The shortest path is along a wire that forms part of the line joining P to the circle's centre, while the steepest path would be tangent to the circle. Some path between these two will mix just the right blend of distance and speed, and you have to determine which one it is.
We all remember from high school that
- wire and air are frictionless;
- Newton informed us that the relationship among distance s, velocity v, and time t of a body under constant acceleration is
s = 1/2vt; and
- if m is the bead's mass, g is gravity, and h is the vertical component of the drop from P to Q, then the potential energy mgh equals 1/2mv2, where v is the velocity of the bead when it reaches Q.
|
 Solution. Solution.
|
| PM74: January 2008 |
 |
What are the positive integers n for which
3n + 4n+ ... + (n+2)n= (n+3)n?
|
 Solution. Solution.
|
| PM73: December 2007 |
 |
For the holiday season we offer a mathemagical party trick you can perform to the amazement of your friends and relatives who will receive a pocket calculator as a gift:
- Tell them to pick a number, any number from 1 to 1000. Call it N.
- Next, tell them to compute 1 plus 1/N plus twice the square root of 1/N; then take the square root of the result and store it into memory by pressing the M+ button.
- Now tell them to compute 1 plus 1/N minus twice the square root of 1/N; then take the square root of the result and add it to memory by again pressing the M+ button.
- Finally, tell them to recall the number in memory by pressing the MR button. (The resulting number, of course, is the sum of the square roots from steps 2 and 3.) At the same time, hand them a sealed envelope you've taken from your pocket, and tell them to open it. Once they read the number inside, tell them
`"That's the number you've got, isn't it?"
Of course, you need to prepare the sealed envelope in advance. Our problem of the month is
What magic number should you put inside?
Please explain your answer.
|
 Solution. Solution.
|
| PM72: November 2007 |
 |
Prove that for every n, the integers 1, 2, 3, ... , 2n – 1, 2n can be partitioned into pairs
{a1, b1}, {a2, b2}, ... , {an, bn}
so that ai + bi is prime for every i.
|
 Solution. Solution.
|
| PM71: October 2007 |
 |
A circle with center O and radius 1 cm rolls around the inside of a triangle whose sides are 6, 8, and 10 cm, always touching one or more of the sides as it rolls. How far does O travel in one complete circuit?
|
 Solution. Solution.
|
| PM70: September 2007 |
 |
Six points have been arranged so that the 15 segments that join them in pairs have different lengths and point in different directions. Prove that one of these segments is the longest side of one of the triangles that are formed and, at the same time, the shortest side of another triangle. Is the same claim true when starting with five points (and the 10 segments joining them in pairs have different lengths and different directions)?
|
 Solution. Solution.
|
|
|
 |

