Solution for December 2007

The Problem:

For the holiday season we offer a mathemagical party trick you can perform to the amazement of your friends and relatives who will receive a pocket calculator as a gift: Tell them to pick a number, any number from 1 to 1000.  Call it N. Next, tell them to compute 1 plus 1/N plus twice the square root of 1/N; then take the square root of the result and store it into memory by pressing the M+ button. Now tell them to compute 1 plus 1/N minus twice the square root of 1/N; then take the square root of the result and add it to memory by again pressing the M+ button. Finally, tell them to recall the number in memory by pressing the MR button. (The resulting number, of course, is the sum of the square roots from steps 2 and 3.)  At the same time, hand them a sealed envelope you've taken from your pocket, and tell them to open it. Once they read the number inside, tell them `"That's the number you've got, isn't it?" Of course, you need to prepare the sealed envelope in advance. Our problem of the month is What magic number should you put inside?  Please explain your answer.

Correct responses:

We received correct submissions for this month's problem from the following people: Theerasak Asawanonwiwat (Thailand) Nouini Kacem (France) Bojan Basic (Serbia) Wolfgang Kais (Germany) Gérard Billion (France) Normand LaLiberté (Ontario) Lou Cairoli (USA) Jean-Luc Luyet (Switzerland) John Campbell (Alberta) Jacques Mertzeisen (France) K.A. Chandrashekara (India) Nikhil V. Nair (India) Dave Denison (Internet) Viktor Pačnik  (Slovenia) Sébastien Dumortier (France) Wilfried Pillard (France) Philippe Fondanaiche (France) John T. Robinson (USA) Alenka Gabrovec (Slovenia) K. Sengupta (India) Xavier Hecquet (France) Heri Setiyawan (Indonesia) Rizwan A. Hussain (Fiji Islands) Steve Sparling (British Columbia) Yitz Itzik (Internet) A. Teitelman (Israel)

The solution:

            The magic number is 2.  Our correspondents discovered the number using one of two similar methods.

            Although it will not change our analysis if we let N be any real number equaling 1 or greater, the statement of our problem clearly implies that N is a positive integer.  Let s = √(1/N) We observe that 0 < s ≤ 1.  The numbers stored in the calculator are then

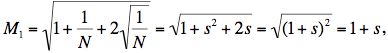
and

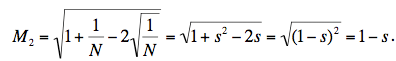
We must be careful here to insure that we are taking the positive square root of a positive number: the first set of equalities are valid because s > 0, while the second works because s ≤ 1.  (Observe that should we have s > 1, then M2 would equal s – 1.)   The magic number is therefore

M = M₁ + M₂ = 1 + s + 1 – s = 2

            Unfortunately, there are calculators that will display 1.9999999 or 2.0000001 instead of 2.  Although most of us understand about rounding errors, such an outcome will certainly diminish the impact of our magic trick.  Of course, professional magicians will have a joke prepared for when their trick flops.  Perhaps we can shift the blame to the poor workmanship that goes into calculators outsourced to some country that will remain nameless because we would not wish to embarrass it shortly before they host the 2008 Olympics.

            Finally, the alternative method is to compute M².  Here it will be convenient to let x = 1/N, so that

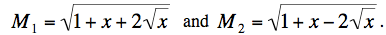
Recalling the product formula

(a + b)(a - b) = a² - b²

when a = 1 + x and b = 2 √x we get

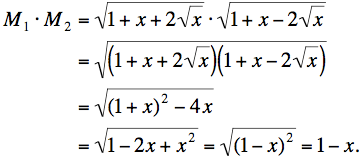
You should take note of the subtlety in the second line.  We require √p · √q = √(pq) which holds only when both p and q are nonnegative.  The conditions on N here—that N ≥ 1—insure that x ≤ 1, and thus p = 1+x+2√x > 0 and q = 1+x–2√x ≥ 0, so that the computation is valid.

            We now compute M²:

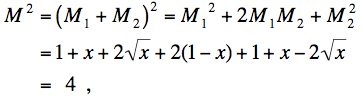
so again we see that M = 2.