|
|
|
Math Central - mathcentral.uregina.ca |
 |
 |
Problem of the Month 2011-2012
|
 |
 |
 |
 |
| PM114: May, 2012 |
 |
An arbitrary permutation $\sigma$ of the set of integers from 1 to 2012 can be represented in the plane by a set of 2012 points of the form $\left(k, \sigma(k)\right)$, where $k$ runs from 1 to 2012. The smallest square bounding this set of points with sides parallel to the coordinate axis has at least 2 and at most 4 points of the set on its boundary. Determine the number of permutations having exactly $m$ points on the boundary for $m$ equal to 2, to 3, and to 4.
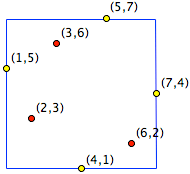
To help you understand the problem, we include an example below of the corresponding figure for when $\sigma$ is a permutation of the numbers from 1 to 7 that has four points on its bounding square, namely the permutation that takes the ordered set $(1, 2, 3, 4, 5, 6, 7)$ to $(5, 3, 6, 1, 7, 2, 4)$.
|
 Solution. Solution.
|
| PM113: April, 2012 |
 |
Recall that the incenter $I$ of a triangle is the point where the three internal angle bisectors meet. Prove that any line through $I$ that divides the area of the triangle in half also divides its perimeter in half; conversely, any line through $I$ that divides the perimeter of the triangle in half also divides its area in half.
|
 Solution. Solution.
|
| PM112: March, 2012 |
 |
Can the sixteen digits
$$2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9$$
be arranged to form two 8-digit numbers $A$ and $B$ with $B= 2A$?
|
 Solution. Solution.
|
| PM111: February, 2012 |
 |
Does there exist a bounded real-valued function $f(x)$ with $f(1) > 0$ such that for all real numbers $x$ and $y$,
$$\left(f(x+y)\right)^2 \ge \left(f(x)\right)^2 + 2f(xy) +\left(f(y)\right)^2 .$$
|
 Solution. Solution.
.
|
| PM110: January, 2012 |
 |
The polynomial $p(x)$ with real coefficients has degree $2011$ and satisfies
$$p(n)=\frac{n}{n+1}$$
for all integers $n,\; 0 \le n \le 2011$. Compute $p(2012)$.
|
 Solution. Solution.
.
|
| PM109: December 2011 |
 |
Find all primes $p$ such that $\large \frac{2^{p-1} -1}{p}$ is a perfect square.
|
 Solution. Solution.
|
| PM108: November 2011 |
 |
- Does there exist a family of circles in the Euclidean plane with positive finite radii such that every point of the plane lies on exactly two of the circles?
- Does there exist a family of circles in the Euclidean plane with positive finite radii such that every point of the plane lies on exactly 100 of the circles?
|
 Solution. Solution.
.
|
| PM107: October 2011 |
 |
Find the smallest positive integer $n$ for which $n^2 + 3n + 5$ is divisible by 121, or prove that no such integer exists.
|
 Solution. Solution.
.
|
| PM106: September 2011 |
 |
Find the positive integers $m$ and $n$ for which the roots of the equations
$$x^2 - mx + (n+1) = 0 \quad \mbox{ and } \quad x^2 - (n+1)x + m = 0$$
are positive integers that, together with $m$ and $n$, form in some order an arithmetic progression whose sum is $21$.
|
 Solution. Solution.
|
|
|
 |

