Solution for November 2011

The Problem:
	Does there exist a family of circles in the Euclidean plane with positive finite radii such that every point of the plane lies on exactly two of the circles? Does there exist a family of circles in the Euclidean plane with positive finite radii such that every point of the plane lies on exactly 100 of the circles?

The solution:

Yes, for both (a) and (b). The problem was posed in 1988 at the Tournoi des villes in France, requiring 1988 circles through each point of the plane. It appeared later in the book Hypermath: 120 exercices de haut vol by Pierre Bornsztein (Vuibert, Paris, 2001). We thank Jean Doyen for showing us the problem.

Correct solutions were submitted by Lamis Alsheikh (Syria), Bernard Collignon (France), Philippe Fondanaiche (France), Jan Fricke (Germany), Benoît Humbert (France), Ile Ilijevski (Macedonia), and Patrick J. LoPresti (USA). We also received three incomplete solutions.

All the submitted solutions were variations of the same idea: use strips of congruent circles. It makes one wonder if there is essentially only one approach to the problem. The family we use in (a)

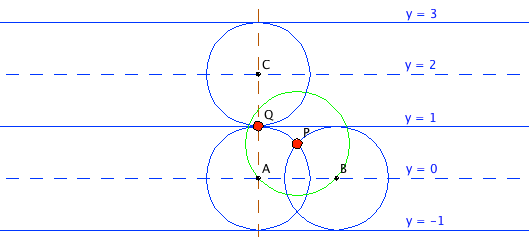
consist of unit circles in horizontal strips: the circles of the family all have radius 1; their centers are the points assigned coordinates $(x,y)$ with $x$ running through the real numbers and $y$ running through the even numbers. The borders of the horizontal strips are the lines $y=n$, where $n$ is an odd number. Two typical strips of width 2 are shown in the accompanying figure. Consider the strip centered on the line $y=0$: any point, say $P$, in the interior of the strip is less than one unit away from $y=0$, whence it is at a unit distance from exactly two points on that line ($PA=PB=1$ in the figure). Those points are the centers of the pair of unit circles of the family through $P$. A point such as $Q$ on the border of a strip is the point where a pair of unit circles are tangent, one from each strip that shares the border, whence $Q$ is on two circles of the family. Since every point of the plane is either in the interior of one such horizontal strip or on its border, every point of the plane is on exactly two circles of the family, as required.

For the answer to (b) we can take 50 copies of the family used above; of course we must make sure that the circles of each of those 50 subfamilies are distinct from those of the other 49 subfamilies. Here are two ways to achieve this. First, we can translate the horizontal lines that form the borders and center lines of part (a) from $y = n$ to $y = n + \frac{j}{50}, \; 0 \le j \le 49$. In this way, the $y$-coordinates of the centers of the unit circles of subfamily $j$ (namely $n + \frac{j}{50}$, $n$ even) will be distinct from those of subfamily $k$ (namely $m + \frac{k}{50}$, $m$ even) when $j \ne k$, whence each point of the plane will lie on exactly two circles of each subfamily. Alternatively, one could obtain the $j$th subfamily by dilating the circles of solution (a) by the factor $j, 1 \le j \le 50$, so that circles of different subfamilies would have different radii.
Further comments.
Everybody noted that the argument for part (b) extends in a natural way to producing a family of circles that cover the points of the plane exactly $N$ times for any nonnegative even number $N$. Humbert and LoPresti noted that $N$ could not taken to be $1$; that is, there exists no family of circles such that every point of the plane lies on exactly one circle of the family. To prove his claim he argued that if, to the contrary, such a family were to exist, then he could define a sequence $C_1, C_2, C_3, \cdots$ of its circles, where $C_1$ is an arbitrarily chosen member of the family and $C_i, i>1,$ is the unique member of the family that contains the center of $C_{i-1}$. Each circle $C_i$ is contained in the interior of all previous circles of the sequence (because it contains the center of $C_{i-1}$ and cannot have a point in common with that circle, as we assume that no point can belong to more than one circle of the family). This implies that for all $i$ the radius of $C_i$ is less than half that of $C_{i-1}$, whence the sequence of circles would shrink to a single point. But that point could not lie on any circle of the family (because such a circle would have to lie in the interior of all the circles $C_i$) contrary to the assumptions that every circle of the family has positive radius, and every point of the plane lies on one of those circles.

Bojan Bašić has sent us a solution that uses transfinite induction to prove that for any $N \ge 2$ there exists a family of circles in the plane such that every point of the plane lies on exactly $N$ circles of the family. It remains, however, an open challenge to produce a deterministic construction of such a family for some $N$ other than $N = 2$; that is, we should be able to list for any point $P$ the centers and radii of those $N$ circles of the family that pass through $P$. Here is Bašić's existence proof.

Let $N \ge 2$ be given. Since there is a continuum of points in the plane, we can index them all by ordinals as $\left\{P_\alpha: \alpha < \mathfrak{c}\right\}$. The required set of circles will be constructed by transfinite induction: we shall construct an increasing chain $C_0 \subseteq C_1 \subseteq C_2 \subseteq \dots \subseteq C_\alpha \subseteq \dots$ of sets of circles such that for each $\alpha < \mathfrak{c}$, $|C_\alpha| \le \aleph_0 \cdot |\alpha|$, the point $P_\alpha$ lies on exactly $N$ circles from $C_\alpha$, and no $N+1$ circles from $C_\alpha$ have a common intersection.

We define the set $C_0$ to consist of an arbitrary selection of $N$ circles passing through the point $P_0$. Assume now that for each ordinal $\beta$ less than a given ordinal $\alpha$ the set $C_\beta$ satisfying the three requirements given above has been constructed. Consider the point $P_\alpha$. It lies on exactly $M$ circles from $\bigcup_{\beta < \alpha}C_\beta$, where $0 \le M \le N$. If $M=N$, let $C_\alpha = \bigcup_{\beta < \alpha}C_\beta$. Assume now that $M<N$. We will choose $N-M$ appropriate radii $R>0$ and add $N-M$ circles with center $P_\alpha - (R,0)$ and radius $R$, avoiding circles that pass through a point $P_\beta$ which already lies on $N$ circles from our construction.
Because two circles have at most two intersection points, and since $\left|\bigcup_{\beta < \alpha}C_\beta\right| \le \sup\{\aleph_0 \cdot |\beta| : \beta < \alpha\} = \aleph_0 \cdot |\alpha|$, there are at most $\aleph_0 \cdot |\alpha| <\mathfrak{c}$ intersection points of circles from $\bigcup_{\beta < \alpha}C_\beta$. Thus there are fewer than a continuum of bad choices for $R$, while we have a continuum of good choices. Finally, let $C_\alpha$ be the union of the set of these $N-M$ circles and $\bigcup_{\beta < \alpha}C_\beta$. Therefore $|C_\alpha| \le \aleph_0 \cdot |\alpha| + (N-M) = \aleph_0 \cdot |\alpha|$; moreover, the point $P_\alpha$ lies on exactly $N$ circles from $C_\alpha$, and no $N+1$ circles from $C_\alpha$ have a common intersection. The set $C = \bigcup_{\alpha < \mathfrak{c}}C_\alpha$ is the required family of circles.