|
|
|
Math Central - mathcentral.uregina.ca |
 |
 |
Problem of the Month 2006-2007
|
 |
 |
 |
 |
| PM69: May 2007 |
 |
Which positive integers n satisfy
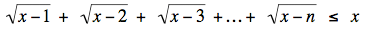
for all real numbers x ≥ n?
|
 Solution. Solution.
|
| PM68: April 2007 |
 |
We say that two points on a sphere are orthogonal if the lines joining those points to the sphere's centre are perpendicular. For example, the North Pole is orthogonal to any point on the equator and to no other points. What is the minimum number of colours required for colouring an entire sphere in such a way that no two orthogonal points have the same colour?
|
 Solution. Solution.
|
| PM67: March 2007 |
 |
Prove that there are infinitely many integers such that
(i) the number is divisible by the sum of its digits, and
(ii) none of its digits are zero.
|
 Solution. Solution.
|
| PM66: February 2007 |
 |
Sophie and Sally each got puzzles for Christmas. Sophie's puzzle was a 10´10 grid to be filled by a certain number of 1×4 tiles and a certain number of 2×2 tiles, with no tiles left over. Sally's puzzle was also a 10×10 grid to be filled by a certain number of 1×4 tiles and a certain number of 2×2 tiles, with no tiles left over. Sophie could complete her puzzle in 2 minutes and 30 seconds, and Sally could complete hers in 4 minutes. Then, they switched, and Sophie completed Sally's puzzle in 4 minutes and 20 seconds while Sally completed Sophie's puzzle in 3 minutes and 12 seconds. Then, they switched back to their own puzzle, but Sophie gave Sally one of her 1×4 tiles, and Sally gave Sophie one of her 2×2 tiles. Our problem: How long will each take to complete her puzzle now?
|
 Solution. Solution.
|
| PM65: January 2007 |
 |
The number 5 × 734 has a great many digits in its decimal representation. Without evaluating those digits, prove that some digit occurs at least four times in the number.
|
 Solution. Solution.
|
| PM64: December 2006 |
 |
For the holiday season we offer a mathemagical party trick to amaze friends and relatives. No special training is required — just a table and 45 coins.

Place your 45 coins on the table and ask for a volunteer to blindfold you (this step is optional) and then to arrange the coins in as many piles of whatever height he wishes. He could, for example, make one pile of 24 coins, one of 20 coins, and one of 1 coin. Tell him to take one coin from each of his piles to make a new pile. (In our example the new pile would have 3 coins and the two old piles that remain would now have 23 and 19 coins.) Instruct him to repeat the process — that is, he should take one coin from each pile (including the new) to form a yet another pile (this gives piles of 22, 18, 3, and 2 in our example) — and to keep repeating it. After a suitable length of time, depending on the starting configuration and the skill of your volunteer, you announce that he has one pile of each size from 1 to 9.
Our problem for December: Prove that this trick always works.
|
 Solution. Solution.
|
| PM63: November 2006 |
 |
We start with two positive real numbers a0 and a1, and obtain an infinite sequence whose terms satisfy
an+1 an-1 = an + 1.
Show that an+ 5 = an for all n.
|
 Solution. Solution.
|
| PM62: October 2006 |
 |
Your task is to convert
x2 + 10 x + 20 into x2 + 20 x + 10
in 50 steps or less, where on each step you are allowed
to add 1 to, or to subtract 1 from, either the current constant term or the coefficient of x (but not both),
subject to the condition that
no change is allowed to produce a polynomial that can be factored into
(x + m)( x + n), where m and n are integers.
For example, the first step cannot reduce the 10 to 9 because
x2 + 9 x + 20 = (x + 5)(x + 4).
|
 Solution. Solution.
|
| PM61: September 2006 |
 |
- 15 chairs are equally spaced around a circular table on which are the name cards for 15 delegates. The delegates fail to notice these cards until after they have sat down and, surprisingly, no one is sitting in front of his own card. Prove that the table can be rotated so that at least two of the delegates are simultaneously correctly seated.
- Give an example of an arrangement in which just one of the 15 delegates is correctly seated and for which no rotation correctly places more than one.
|
 Solution. Solution.
|
|
|
 |

