A.W. Hales and E.G. Straus. Projective colorings. Pac. J. Math. 99:31-43, 1982,

C. D. Godsil and J. Zaks. Coloring the sphere. University of Waterloo research report CORR 88-12, 1988

Other references can be found on the web page

 http://tph.tuwien.ac.at/~svozil/publ/blatter.htm.

Among other things, Godsil and Zaks prove that the points of the unit sphere that have rational coordinates can be coloured with only three colours in such a way that orthogonal points have different colours.  Since the infinitely many rational points are dense in the sphere, their result seems to contradict the answer to our problem; at least it makes it clear that some work is required to prove that three colours are insufficient.

Part 1: Three colours are not sufficient.
            Here is Matthew Lim's way of showing the insufficiency of three colours.  Suppose, to the contrary, that we could 3-colour the unit sphere x² + y² + z² = 1 so that orthogonal points got different colours.  Then any great circle (that is, any circle whose plane contains the origin) must have at least two colours (because it contains pairs of orthogonal points), but it cannot use all three colours because its two poles (the points orthogonal to all points of the great circle) must get the third colour.  The points

I = (1, 0, 0),   J = (0, 1, 0),   and K = (0, 0, 1)

are mutually orthogonal, so they must receive different colours, say red, blue, and green, respectively.  Consider

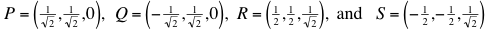
as shown in the schematic diagram. 

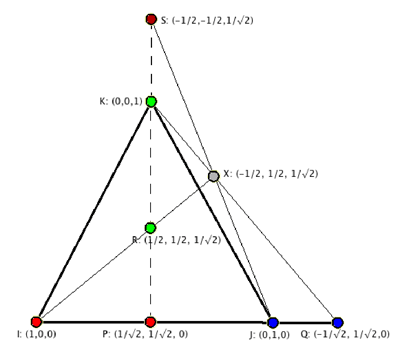
Because P and Q are orthogonal, they must have different colours; because they are on the great circle determined by I and J, their colours are red and blue.  We assume for the moment that P is red and Q is blue.  Similarly, R and S are orthogonal points on the great circle determined by P and K; we will assume that R is green and S is red.  Consider the point X with coordinates (-1/2, 1/2, 1/√2): X lies on the great circle

IR determined by the plane z = √2 y, so its colour must be red or green;
JS determined by the plane z = -√2 x , so its colour must be red or blue;
KQ determined by the plane y = –x, so its colour must be blue or green.

Since X cannot satisfy all three conditions simultaneously, the proposed 3-colouring is not possible. 
         But what if the colours of P and Q, or of R and S, had been switched.  In any case we could simply relabel the points so that the above argument would go through with minor changes: we can replace I by its antipodal point I' = (–1, 0, 0) (it will also be red because antipodal points would necessarily have the same colour in a 3-colouring); in this case Q would be a red point on the short arc between the red I' and the blue J, so we would place R and S on the great circle QK, reversing the roles of P and Q.  Similarly, if R had been red instead of green, we would replace it and K with the antipodal points of S and K.  In all cases we would arrive at a point X that could not be properly coloured, and conclude that three colours are not sufficient to colour the sphere so that all orthogonal points are coloured differently.

Part 2: Four colours are sufficient.
We will use Billion's rule for colouring the top half of the sphere, and complete the job using the rule that antipodal points receive the same colour.  The first figure shows the open spherical triangles above each quadrant in the xy-plane receiving the colours yellow (above x, y > 0), red (above x < 0, y > 0), blue (above x, y < 0), and green (above x > 0, y < 0).  The second figure shows the north pole (blue), four points that define quadrants on the equator (two yellow, two red), and the eight open arcs of the great circles that join these points.  One must check that for each point depicted in each of the figures, the great circle that is orthogonal to it is composed of different colours.

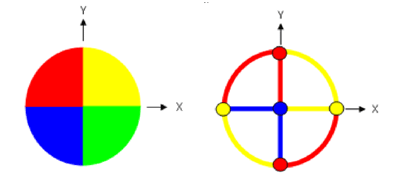
Views of the sphere from above the north pole.