as required.
For n = 2 and x ≥ 2, start with (x – 2)2 ≥ 0, which implies x2≥ 4x – 4. Taking the square root of both sides yields
as required.
For n ≥ 3 the inequality fails for appropriate values of x. In fact, it always fails for x = n + 1. We base our proof of the claim on two very simple inequalities:
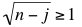for j running from 0 to n – 1, and-
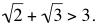
(To verify this inequality one can use a calculator, or note that since
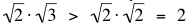
, it follows that
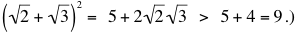
Proof that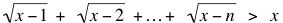 
when x = n + 1:
Comments.
In addition to solving our problem, John Robinson investigated the behavior of the difference between x and the sum of the square roots, namely
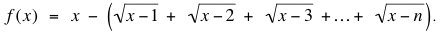
As we saw above, for n ≥ 3 the function is negative when x = n+1; moreover, it is clearly positive for large x, say x > n2. Robinson was able to show that f(x) switches from negative to positive around n2– n/2. More precisely, when n > 4 and x is an integer,
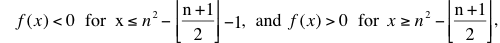
where floor brackets designate the greatest integer less than or equal to the number they enclose. So, for example, setting n = 5 and x = 52 – (5 + 1)/2, we get
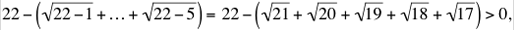
while
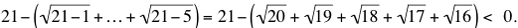
He managed to show this by replacing each square root by its second degree Taylor polynomial
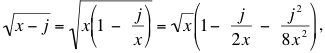
Meanwhile, Matthew Lim wondered what sort of result holds when the square roots in our problem are replaced by kth roots. He was able to show (by induction) that as with square roots, for n ≥ 2k – 1 and x = n + 1, we have
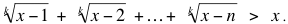
He was, however, unable to say anything about how the sum compares to x when n < 2k – 1, except in the case of our problem (where k = 2).
