We received correct solutions from:
Saïd Amghibech (Québec) |
|
Wolfgang Kais (Germany) |
Mario Antunez (Honduras) |
|
Normand LaLiberté (Ontario) |
Ricardo Barroso Campos (Spain) |
|
Matthew Lim (USA) |
Pierre Bornsztein (France) |
|
Juan Mir Pieras (Spain) |
Bernard Carpentier (France) |
|
Nikhil V. Nair (India) |
K.A. Chandrashekara (India) |
|
Wilfrid Pillard (France) |
Stefaan De Winter (Belgium) |
|
Mark Pilloff (USA) |
Sébastien Dumortier (France) |
|
Manoranjan Sahu (India) |
Philippe Fondanaiche (France) |
|
Shiv Mohan Sharma (internet) |
Baptiste Gorin (France) |
|
A. Teitelmam (Israel) |
Xavier Hecquet (France) |
|
Zac Friggstad (Alberta) |
We received a variety of solutions, but most correspondents were satisfied using a straightforward argument. We present such a solution first, followed by two simplified versions. The sequence itself is related to some ideas of Gauss; we will conclude with his treatment of the problem, including his proof by deus ex machina.
The straightforward solution. Since we need only six letters, let us replace six successive elements an, ... , an+5 of the sequence by the letters in order from u to z. In this notation we are given the four equations
(1) uw = v+1, (2) vx = w+1, (3) wy = x+1, (4) xz = y+1,
and are to prove that z = u.
From (1) we get 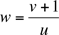 .
.
Plug this value of w into (2), and continue in this way to get successively,
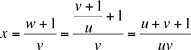
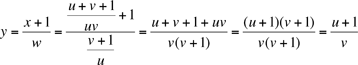
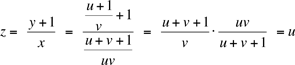
Thus we have z = u, so that an+5 = an for any n, as desired. Since all terms are positive, we never have to worry about dividing by zero, so that each step is valid. As Mir points out, we can relax the positivity condition by simply requiring that a0 + 1 ≠ 0 , a1 + 1 ≠ 0, and a0 + a1 + 1 ≠ 0.
A shortcut from Saïd Amghibech (that we modified somewhat).
We use the same notation as in the first solution. Multiply equation (4) by w to get
wxz =(4) wy + w =(3) x + 1 + w =(2) x + xv = x(1 + v) =(1) xuw
Cancel the wx from both sides to conclude that z = u.
We can find another easy solution by noticing that the given condition is symmetric in n+1 and n-1; in other words, the formula for increasing n is the same as for decreasing n. That suggests we start in the middle, letting an = w and an+1 = x. We then have
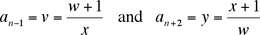
from which we get (as in the first solution)
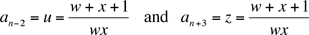
Thus, we get an-2 = an+3 for all n, which is another way of saying that the sequence is a 5-cycle.
A solution from Gauss.
In truth, Gauss did not send us his solution. We got it from H.S.M. Coxeter in his article, "Frieze Patterns", Acta Arithmetica 26 (1971), pages 297-310. See pages 297 and 298. In Coxeter's words,
The story begins in 1602, when Nathaniel Torporley (1564-1632) began to investigate the five "parts" a, A, b, B, c of a right-angled spherical triangle (right-angled at C). According to De Morgan, Torporley anticipated by a dozen years the famous rules of Napier which Gauss embodied in his pentagramma mirificum. [Napier's rules allows one to derive a large portion of spherical trigonometry with very little effort; see, for example, what the Wikipedia has to say about Napier and his rules.] Gauss used the identity
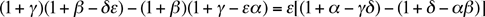
to prove that any three of the four relations

implies the remaining one and also 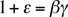 .
.

