Solution to October 2006 Problem

Problem:
Your task is to convert

x² + 10 x + 20 into x² + 20 x + 10  

in 50 steps or less, where on each step you are allowed

to add 1 to, or to subtract 1 from, either the current constant term or the coefficient of x (but not both),

subject to the condition that

no change is allowed to produce a polynomial that can be factored into
(x + m)( x + n), where m and n are integers. 

For example, the first step cannot reduce the 10 to 9 because
x² + 9 x + 20 = (x + 5)(x + 4).

Solution.
         Fondanaiche suggested we turn the task over to Sisyphus to keep him busy when he tires of rolling his stone up the hill.  A few correspondents referred to their task as "Mission Impossible"!  But, of course, the mission-impossible team always manages to accomplish their mission.  Here even the great Tom Cruise would fail.  It can't be done, even if we allow extra steps.  There were two basic approaches.

The algebraic solution.  (This version is based on similar solutions from Bornsztein, Carpentier, Fondanaiche, and Kais.)
         Let p be the current coefficient of x and q the constant term, and consider their difference d = p – q.  On each step d changes by +1 or by –1.  At the start d = –10, while at the finish d must equal +10.  Therefore, somewhere along the way this difference would take a value of 1.  The resulting polynomial would then be x² + (q+1)x + q for some integer q.  Unfortunately, x² + (q+1)x + q = (x + q)(x + 1) with q and 1 integers, which is not allowed. 

The geometric solution. (This version comes mostly from Mir, with ideas from other similar solutions.)
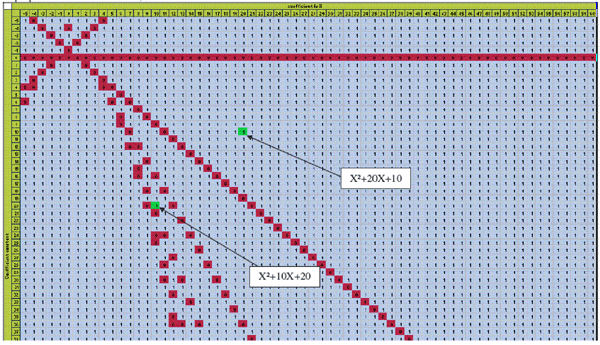
         We can assign the polynomial x² + px + q to the square with coordinates (p, q) in an infinite chessboard.  At each step we move one square right or left, up or down (but not diagonally). Colour each square red that corresponds to a polynomial that can be factored into (x + m)(x + n) where m and n are integers.  Our task is to move from the square (10, 20) to the square (20, 10) one step at a time without entering a red square.  This can never be done because there is a full red diagonal (q+1, q) between those two squares. 
         Dumortier, Chandrashekara, and Hecquet each attached a picture that shows a portion of the chessboard.  Dumortier's picture shown below indicates squares that correspond to factorable polynomials by 0 and colours them red; for polynomials that are irreducible over the integers he marks the corresponding square 1 and colours it blue.

click image to enlarge